Buchstab identity
A form of the Sylvester inclusion-and-exclusion principle specialized to sieve theory (cf. also Sieve method). Let 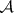 be a finite integer sequence and, for any integer
be a finite integer sequence and, for any integer 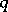 , denote by
, denote by 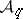 the subsequence of elements of
the subsequence of elements of 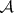 that are multiples of
that are multiples of 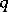 . Let
. Let  be a set of prime numbers (cf. also Prime number), and, for
be a set of prime numbers (cf. also Prime number), and, for 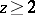 , let
, let 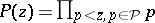 . Finally, let
. Finally, let
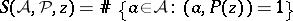 |
denote the "sifting function" associated with 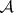 and
and 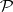 . The Bukhstab identity asserts that, for
. The Bukhstab identity asserts that, for  ,
,
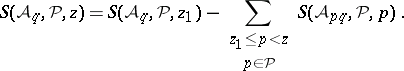 | (a1) |
The identity is useful for deriving a lower-bound sieve estimate from an upper bound sieve estimate (or vice versa) as follows. If the parameter 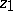 is sufficiently small, then the quantity
is sufficiently small, then the quantity 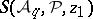 on the right-hand side of (a1) usually can be estimated asymptotically. Thus, if an upper bound for each of the terms
on the right-hand side of (a1) usually can be estimated asymptotically. Thus, if an upper bound for each of the terms 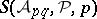 on the right-hand side of (a1) is known, then a lower bound for the sifting function on the left-hand side of (a1) can be deduced.
on the right-hand side of (a1) is known, then a lower bound for the sifting function on the left-hand side of (a1) can be deduced.
References
| [a1] | H. Halberstam, H.-E. Richert, "Sieve methods" , Acad. Press (1974) |
Buchstab identity. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Buchstab_identity&oldid=13771