Degenerate game
separable game, polynomial-like game
A non-cooperative game of  persons in which the pay-off function
persons in which the pay-off function 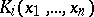 of each player
of each player 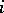 is degenerate, i.e. has the form
is degenerate, i.e. has the form
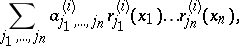 |
where 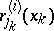 ,
, 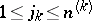 , are functions defined on the set of pure strategies
, are functions defined on the set of pure strategies 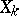 of player
of player 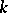 ,
,  . In the case of two-person zero-sum degenerate games on the unit square the pay-off function
. In the case of two-person zero-sum degenerate games on the unit square the pay-off function 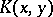 of player I is
of player I is
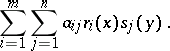 |
Such a game is reduced to a finite two-person zero-sum convex game 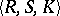 , where
, where 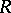 is the convex set spanned by the
is the convex set spanned by the 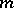 -dimensional curve
-dimensional curve 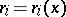 ,
, 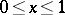 ,
, 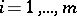 , in
, in 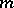 -dimensional space, while
-dimensional space, while 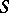 is the convex set spanned by the curve
is the convex set spanned by the curve 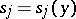 ,
, 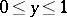 ,
, 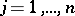 , in
, in  -dimensional space; the pay-off function
-dimensional space; the pay-off function 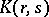 has the form
has the form
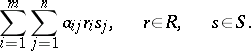 |
In particular, if 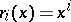 and
and 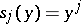 , the degenerate game is called a polynomial game. In any two-person zero-sum degenerate game on the unit square player I has an optimal mixed strategy whose support consists of at most
, the degenerate game is called a polynomial game. In any two-person zero-sum degenerate game on the unit square player I has an optimal mixed strategy whose support consists of at most 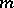 points and if the game is polynomial — of at most
points and if the game is polynomial — of at most  points (in computing the number of points the weight assigned to a terminal point is
points (in computing the number of points the weight assigned to a terminal point is  ). In a similar manner, player II has an optimal mixed strategy whose support consists of at most
). In a similar manner, player II has an optimal mixed strategy whose support consists of at most  points, and in the case of a polynomial game — of at most
points, and in the case of a polynomial game — of at most 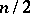 points.
points.
References
| [1] | M. Dresher, S. Karlin, L.S. Shapley, "Polynomial games" , Contributions to the theory of games I , Ann. Math. Studies , 24 , Princeton Univ. Press (1950) pp. 161–180 |
| [2] | D. Gale, O. Gross, "A note on polynomial and separable games" Pacific J. Math. , 8 : 4 (1958) pp. 735–741 |
Degenerate game. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Degenerate_game&oldid=13740