Distribution modulo one
The distribution of the fractional parts 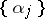 of a sequence of real numbers
of a sequence of real numbers 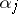 ,
, 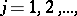 in the unit interval
in the unit interval 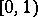 . The sequence of fractional parts
. The sequence of fractional parts 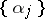 ,
, 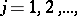 is called uniformly distributed in
is called uniformly distributed in 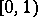 if the equality
if the equality
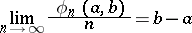 |
holds for any interval 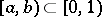 , where
, where 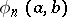 is the number of terms among the first
is the number of terms among the first  members of
members of 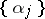 ,
, 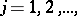 which belong to
which belong to 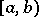 . In this case the sequence
. In this case the sequence 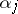 ,
, 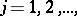 is said to be uniformly distributed modulo one.
is said to be uniformly distributed modulo one.
Weyl's criterion (see [1]) for a distribution modulo one to be uniform: An infinite sequence of fractional parts 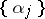 ,
, 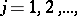 is uniformly distributed in the unit interval
is uniformly distributed in the unit interval 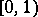 if and only if
if and only if
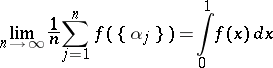 |
for any function 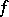 that is Riemann integrable on
that is Riemann integrable on 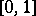 . This is equivalent to the following. In order that a sequence
. This is equivalent to the following. In order that a sequence 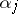 ,
, 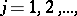 be uniformly distributed modulo one, it is necessary and sufficient that
be uniformly distributed modulo one, it is necessary and sufficient that
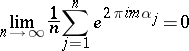 |
for any integer 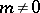 . It follows from Weyl's criterion and his estimates for trigonometric sums involving a polynomial
. It follows from Weyl's criterion and his estimates for trigonometric sums involving a polynomial 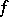 ,
,
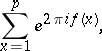 |
that the sequence 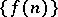 ,
, 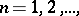 of fractional parts is uniformly distributed in
of fractional parts is uniformly distributed in 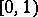 provided that at least one coefficient
provided that at least one coefficient 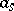 ,
, 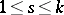 , of the polynomial
, of the polynomial
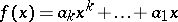 |
is irrational.
The concept of uniform distribution modulo one can be made quantitative by means of the quantity
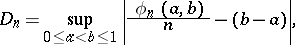 |
called the discrepancy of the first  members of the sequence
members of the sequence 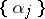 ,
, 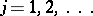 (see [2], [3]).
(see [2], [3]).
References
| [1] | H. Weyl, "Ueber die Gleichverteilung von Zahlen mod Eins" Math. Ann. , 77 (1916) pp. 313–352 |
| [2] | I.M. Vinogradov, "The method of trigonometric sums in the theory of numbers" , Interscience (1954) (Translated from Russian) |
| [3] | L.-K. Hua, "Abschätzungen von Exponentialsummen und ihre Anwendung in der Zahlentheorie" , Enzyklopaedie der Mathematischen Wissenschaften mit Einschluss ihrer Anwendungen , 1 : 2 (1959) (Heft 13, Teil 1) |
Comments
References
| [a1] | E. Hlawka, "Theorie der Gleichverteilung" , B.I. Wissenschaftverlag Mannheim (1979) |
| [a2] | L. Kuipers, H. Niederreiter, "Uniform distribution of sequences" , Wiley (1974) |
Distribution modulo one. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Distribution_modulo_one&oldid=13739