Antipodes
From Encyclopedia of Mathematics
Diametrically-opposite points on a sphere. Borsuk's antipodal-point theorems apply [1]: 1) For any continuous mapping of the sphere 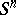 into the Euclidean space
into the Euclidean space 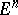 there exist antipodes with a common image; 2) Any mapping of the sphere
there exist antipodes with a common image; 2) Any mapping of the sphere 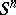 into itself in which the images of antipodes are antipodes is an essential mapping.
into itself in which the images of antipodes are antipodes is an essential mapping.
References
| [1] | K. Borsuk, "Drei Sätze über die  -dimensionale euklidische Sphäre" Fund. Math. , 20 (1933) pp. 177–190 -dimensionale euklidische Sphäre" Fund. Math. , 20 (1933) pp. 177–190 |
Comments
The first result mentioned above is known as the Borsuk–Ulam theorem (on antipodes). The following result also goes by the name of Borsuk's antipodal theorem: There is no continuous mapping 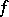 of the
of the 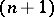 -ball
-ball 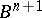 into the
into the  -sphere
-sphere 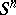 such that
such that 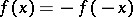 , cf. [a1], p. 131.
, cf. [a1], p. 131.
References
| [a1] | V.I. Istrătescu, "Fixed point theory" , Reidel (1981) |
How to Cite This Entry:
Antipodes. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Antipodes&oldid=13716
Antipodes. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Antipodes&oldid=13716
This article was adapted from an original article by A.V. Chernavskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article