Pettis integral
An integral of a vector-valued function with respect to a scalar measure, which is a so-called weak integral. It was introduced by B.J. Pettis [1].
Let 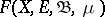 be the vector space of functions
be the vector space of functions 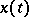 ,
, 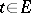 , with values in the Banach space
, with values in the Banach space 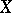 and given on a set
and given on a set 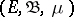 with a countably-additive measure
with a countably-additive measure 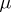 on the
on the 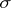 -algebra
-algebra 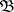 of subsets of
of subsets of 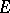 . The function
. The function 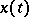 is called weakly measurable if for any
is called weakly measurable if for any 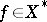 the scalar function
the scalar function 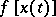 is measurable. The function
is measurable. The function 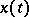 is Pettis integrable over a measurable subset
is Pettis integrable over a measurable subset 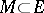 if for any
if for any 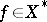 the function
the function 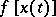 is integrable on
is integrable on 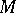 and if there exists an element
and if there exists an element 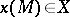 such that
such that
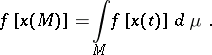 |
Then, by definition,
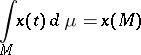 |
is called the Pettis integral. That integral was introduced for the case 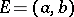 with the ordinary Lebesgue measure by I.M. Gel'fand [2].
with the ordinary Lebesgue measure by I.M. Gel'fand [2].
References
| [1] | B.J. Pettis, "On integration in vector spaces" Trans. Amer. Math. Soc. , 44 : 2 (1938) pp. 277–304 |
| [2] | I.M. Gel'fand, "Sur un lemme de la théorie des espaces linéaires" Zap. Naukovodosl. Inst. Mat. Mekh. Kharkov. Mat. Tov. , 13 : 1 (1936) pp. 35–40 |
| [3] | T. Hildebrandt, "Integration in abstract spaces" Bull. Amer. Math. Soc. , 59 (1953) pp. 111–139 |
| [4] | E. Hille, R.S. Phillips, "Functional analysis and semi-groups" , Amer. Math. Soc. (1957) |
Comments
References
| [a1] | J. Diestel, J.J. Uhl jr., "Vector measures" , Math. Surveys , 15 , Amer. Math. Soc. (1977) |
| [a2] | M. Talagrand, "Pettis integral and measure theory" , Mem. Amer. Math. Soc. , 307 , Amer. Math. Soc. (1984) |
| [a3] | K. Bichteler, "Integration theory (with special attention to vector measures)" , Lect. notes in math. , 315 , Springer (1973) |
Pettis integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pettis_integral&oldid=13712