Bessel system
A concept in the theory of orthogonal systems. Let  and
and  be two complete systems of functions in
be two complete systems of functions in  (i.e. measurable functions that are square-integrable on the segment
(i.e. measurable functions that are square-integrable on the segment  ), forming a biorthogonal system of functions. The system
), forming a biorthogonal system of functions. The system  is said to be a Bessel system if, for any function
is said to be a Bessel system if, for any function  , the series
, the series
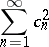 |
is convergent; here,  are the coefficients of the expansion
are the coefficients of the expansion
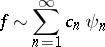 |
of the function 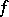 with respect to the system
with respect to the system 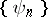 . For a system
. For a system 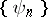 to be a Bessel system it is necessary and sufficient that it be possible to define a bounded linear operator
to be a Bessel system it is necessary and sufficient that it be possible to define a bounded linear operator 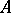 on the space
on the space  such that the system
such that the system 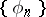 defined by the equation
defined by the equation 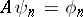 (
( ) is a complete orthonormal system. If the system
) is a complete orthonormal system. If the system 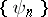 is a Bessel system, there exists a constant
is a Bessel system, there exists a constant 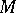 such that for any
such that for any 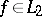
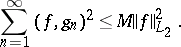 |
References
| [1] | S. Kaczmarz, H. Steinhaus, "Theorie der Orthogonalreihen" , Chelsea, reprint (1951) |
Bessel system. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bessel_system&oldid=13693