Jacobi principle

principle of stationary action

An integral variational principle in mechanics that was established by C.G.J. Jacobi [1] for holonomic conservative systems. According to the Jacobi principle, if the initial position 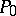and the final position 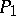of a holonomic conservative system are given, then for the actual motion the Jacobi action

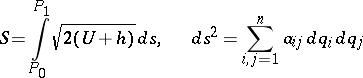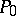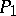has a stationary value in comparison with all other infinitely-near motions between and with the same constant value 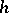of the energy as in the actual motion. Here is the force function of the active forces on the system, and are the generalized Lagrange coordinates of the system, whose kinetic energy is

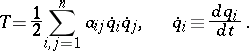Jacobi proved (see [1]) that if and are sufficiently near to one another, then for the actual motion the action 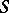has a minimum. The Jacobi principle reduces the problem of determining the actual trajectory of a holonomic conservative system to the geometrical problem of finding, in a Riemannian space with the metric

an extremal of the variational problem.

See also Variational principles of classical mechanics.

References

[1]	C.G.J. Jacobi, "Vorlesungen über Dynamik" , G. Reimer (1884)

References

[a1]	V.I. Arnol'd, "Mathematical methods of classical mechanics" , Springer (1978) (Translated from Russian)