Arguesian lattice
Desarguesian lattice
A lattice in which the Arguesian law is valid, i.e. for all  ,
, 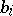 ,
,
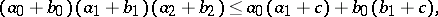 |
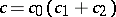 ,
, 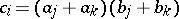 for any permutation
for any permutation 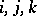 [a21]. Arguesian lattices form a variety (cf. also Algebraic systems, variety of), since within lattices
[a21]. Arguesian lattices form a variety (cf. also Algebraic systems, variety of), since within lattices 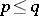 is equivalent to
is equivalent to 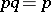 . A lattice is Arguesian if and only if it is a modular lattice and
. A lattice is Arguesian if and only if it is a modular lattice and 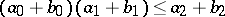 (central perspectivity) implies
(central perspectivity) implies 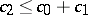 (axial perspectivity). In an Arguesian lattice and for
(axial perspectivity). In an Arguesian lattice and for 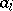 ,
, 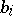 such that
such that 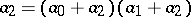 and
and 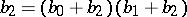 , the converse implication is valid too [a24]. A lattice is Arguesian if and only if its partial order dual is Arguesian.
, the converse implication is valid too [a24]. A lattice is Arguesian if and only if its partial order dual is Arguesian.
Examples of Arguesian lattices.
1) The lattice  of subspaces of a projective space
of subspaces of a projective space 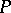 is Arguesian if and only if the Desargues assumption is satisfied in
is Arguesian if and only if the Desargues assumption is satisfied in 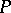 .
.
2) Every lattice 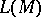 of submodules of an
of submodules of an 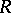 -module
-module 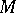 (cf. also Module) and any lattice of subobjects of an object in an Abelian category.
(cf. also Module) and any lattice of subobjects of an object in an Abelian category.
3) Every lattice of normal subgroups (respectively, congruence relations; cf. Normal subgroup; Congruence (in algebra)) of a group and any lattice of permuting equivalence relations [a21] (also called a linear lattice).
4) Considering all lattices of congruence relations of algebraic systems (cf. Algebraic system) in a variety, the Arguesian law is equivalent to the modular law.
5) Every  -distributive modular lattice (cf. also Distributive lattice):
-distributive modular lattice (cf. also Distributive lattice): 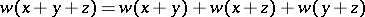 , i.e. without a projective plane in the variety.
, i.e. without a projective plane in the variety.
The Arguesian law can be characterized in terms of forbidden subconfigurations, but not in terms of sublattices [a17]. Weaker versions involve less variables and higher-dimensional versions have increasing strength and number of variables; all are valid in linear lattices [a10]. The basic structure theory relies on the modular law, cf. Modular lattice and [a3], [a27]. For its role in the congruence and commutator theory of algebraic systems, cf. [a12]. Large parts of dimension theory for rings and modules can be conveniently done within modular lattices [a29].
Projective spaces.
See [a16]. Every modular lattice with complements (cf. Lattice with complements) can be embedded into 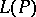 for a projective space on the set
for a projective space on the set 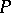 of its maximal filters (cf. Filter), actually a sublattice of the ideal lattice of the filter lattice (with filters ordered by inverse inclusion), whence preserving all identities. This Frink embedding generalizes the Stone representation theorem for Boolean algebras (cf. Boolean algebra). The coordinatization theorem of projective geometry implies that any Arguesian relatively complemented lattice can be embedded into a direct product of lattices of subspaces of vector spaces (cf. Vector space) [a22].
of its maximal filters (cf. Filter), actually a sublattice of the ideal lattice of the filter lattice (with filters ordered by inverse inclusion), whence preserving all identities. This Frink embedding generalizes the Stone representation theorem for Boolean algebras (cf. Boolean algebra). The coordinatization theorem of projective geometry implies that any Arguesian relatively complemented lattice can be embedded into a direct product of lattices of subspaces of vector spaces (cf. Vector space) [a22].
A compact element 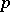 of a modular algebraic lattice
of a modular algebraic lattice 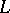 is called a point if it is completely join irreducible, i.e. has a unique lower cover
is called a point if it is completely join irreducible, i.e. has a unique lower cover 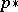 . If each element of
. If each element of 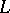 is a join of points (e.g., if
is a join of points (e.g., if 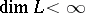 ), then
), then 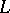 can be understood as the subspace lattice of an ordered linear space on the set
can be understood as the subspace lattice of an ordered linear space on the set 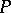 of points: the order is induced by
of points: the order is induced by 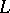 . Points
. Points 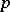 ,
, 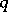 ,
,  are collinear if they are distinct and
are collinear if they are distinct and 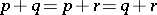 , and a subspace is a subset
, and a subspace is a subset 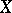 such that
such that 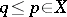 implies
implies 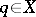 , and
, and 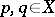 with
with 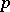 ,
, 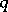 ,
,  collinear implies
collinear implies 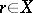 . This can also be viewed as a presentation of
. This can also be viewed as a presentation of 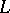 as a semi-lattice. Instead of all collinearities one may use a base of lines: for each element
as a semi-lattice. Instead of all collinearities one may use a base of lines: for each element 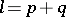 a maximal set of points with pairwise join
a maximal set of points with pairwise join 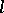 . For an abstract ordered linear space one has to require that collinearity is a totally symmetric relation, that collinear points are incomparable, that
. For an abstract ordered linear space one has to require that collinearity is a totally symmetric relation, that collinear points are incomparable, that 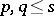 and
and 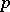 ,
, 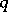 ,
,  collinear implies
collinear implies 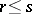 , that for
, that for 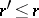 and
and 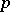 ,
, 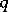 ,
,  collinear there are
collinear there are 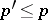 and
and 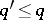 such that
such that 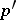 ,
, 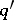 ,
, 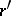 are collinear or
are collinear or 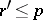 or
or 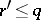 , and, finally, a more elaborate version of the triangle axiom. Then the subspaces form a lattice
, and, finally, a more elaborate version of the triangle axiom. Then the subspaces form a lattice 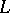 as above and each modular lattice can be naturally embedded into such, preserving identities.
as above and each modular lattice can be naturally embedded into such, preserving identities.
Subdirect products and congruences.
See [a3], [a20]. Every lattice is a subdirect product of subdirectly irreducible homomorphic images (cf. Homomorphism). By Jónsson's lemma, the subdirect irreducibles in the variety generated by a class 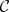 are homomorphic images of sublattices of ultraproducts from
are homomorphic images of sublattices of ultraproducts from 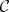 . A pair of complementary central elements
. A pair of complementary central elements  ,
,  provides a direct decomposition
provides a direct decomposition 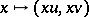 , a neutral element
, a neutral element  implies a subdirect decomposition
implies a subdirect decomposition 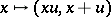 .
.
Any congruence 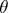 on a modular lattice
on a modular lattice 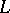 is determined by its set
is determined by its set 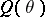 of quotients, where a quotient is a pair
of quotients, where a quotient is a pair 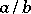 with
with 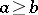 , equivalently, an interval
, equivalently, an interval 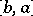 . A pair of quotients is projective if it belongs to the equivalence relation generated by
. A pair of quotients is projective if it belongs to the equivalence relation generated by 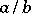 ,
, 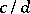 such that
such that 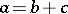 and
and 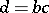 . A subquotient
. A subquotient 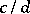 of
of 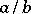 is such that
is such that 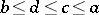 . If
. If 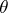 is generated by a set
is generated by a set 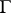 of quotients, then
of quotients, then 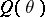 is the transitive closure of the set of all quotients projective to some subquotient of a quotient in
is the transitive closure of the set of all quotients projective to some subquotient of a quotient in 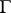 . The congruences form a Brouwer lattice, with the pseudo-complement
. The congruences form a Brouwer lattice, with the pseudo-complement 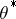 of
of 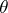 given by the quotients not having any subquotient projective to a subquotient of a quotient in
given by the quotients not having any subquotient projective to a subquotient of a quotient in 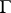 .
. 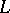 is subdirectly decomposed into
is subdirectly decomposed into 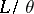 and
and 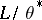 and each subdirectly indecomposable factor of
and each subdirectly indecomposable factor of 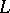 is a homomorphic image of
is a homomorphic image of 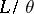 or
or 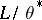 . If
. If 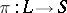 is onto,
is onto, 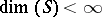 , and if
, and if 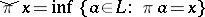 (which then preserves sups) and the dual
(which then preserves sups) and the dual 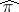 exist, i.e. for a bounded image, then for
exist, i.e. for a bounded image, then for 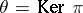 one finds that
one finds that 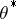 is the transitive closure of prime quotients
is the transitive closure of prime quotients 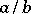 with
with 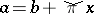 ,
, 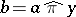 for some prime quotient
for some prime quotient 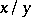 in
in 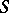 . For any onto mapping
. For any onto mapping 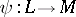 with
with 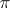 not factoring through
not factoring through 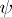 , this splitting method yields the relations
, this splitting method yields the relations 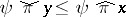 for prime quotients
for prime quotients 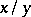 in
in 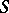 . If
. If 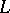 is generated by a finite set
is generated by a finite set 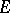 , starting with
, starting with 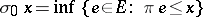 and iterating,
and iterating, 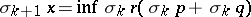 with
with 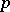 ,
,  ,
,  ranging over all subtriples of lines of a given base, leads to
ranging over all subtriples of lines of a given base, leads to 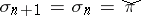 for some
for some  [a28].
[a28].
For 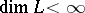 , each congruence is determined by its prime quotients, either those in a given composition sequence or those of the form
, each congruence is determined by its prime quotients, either those in a given composition sequence or those of the form 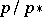 ,
, 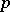 a point. It follows that the congruences form a finite Boolean algebra and are in one-to-one correspondence with unions of connected components of the point set under the binary relation:
a point. It follows that the congruences form a finite Boolean algebra and are in one-to-one correspondence with unions of connected components of the point set under the binary relation: 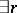 with
with 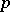 ,
,  ,
,  collinear. Moreover, the subdirectly indecomposable factors
collinear. Moreover, the subdirectly indecomposable factors 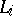 of
of 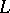 are simple, i.e. correspond to maximal congruences
are simple, i.e. correspond to maximal congruences 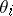 , and the dimensions add up:
, and the dimensions add up: 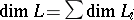 . The connected components associated with the
. The connected components associated with the 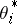 are disjoint and are isomorphic images of the spaces of the
are disjoint and are isomorphic images of the spaces of the 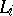 via
via 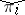 . Thus, the space of
. Thus, the space of 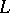 can be constructed as the disjoint union of the spaces of the
can be constructed as the disjoint union of the spaces of the 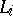 with
with 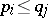 if and only if
if and only if 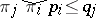 where
where 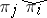 depends only on the subdirect product of
depends only on the subdirect product of 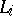 and
and 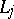 and can be computed, in the scaffolding construction, as the pointwise largest sup-homomorphism
and can be computed, in the scaffolding construction, as the pointwise largest sup-homomorphism 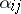 of
of 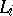 into
into 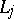 such that
such that 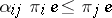 for a given set of generators
for a given set of generators  .
.
Glueing.
See [a8]. A tolerance relation on a lattice 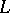 is a binary relation that is reflexive, symmetric, and compatible, i.e. a subalgebra of
is a binary relation that is reflexive, symmetric, and compatible, i.e. a subalgebra of 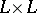 . A block is a maximal subset with every pair of elements in relation, whence a convex sublattice. The set
. A block is a maximal subset with every pair of elements in relation, whence a convex sublattice. The set 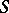 of blocks has a lattice structure. A convenient way to think of this is as a pair
of blocks has a lattice structure. A convenient way to think of this is as a pair 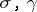 of embeddings of a (not necessarily modular) skeleton lattice
of embeddings of a (not necessarily modular) skeleton lattice 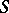 into the filter, respectively ideal, lattice of
into the filter, respectively ideal, lattice of 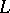 preserving finite sups, respectively infs, such that
preserving finite sups, respectively infs, such that 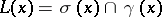 is non-empty for each
is non-empty for each  , namely one of the blocks. A relevant tolerance for modular lattices is given by the relation that
, namely one of the blocks. A relevant tolerance for modular lattices is given by the relation that 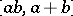 be complemented. Its blocks are the maximal relatively complemented convex sublattices of
be complemented. Its blocks are the maximal relatively complemented convex sublattices of 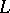 , and
, and 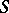 is then the prime skeleton. One has a glueing if the smallest congruence extending the tolerance is total; this occurs for modular
is then the prime skeleton. One has a glueing if the smallest congruence extending the tolerance is total; this occurs for modular 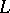 of
of 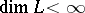 and the prime skeleton tolerance. The neutrality of
and the prime skeleton tolerance. The neutrality of 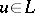 can be shown with suitable
can be shown with suitable 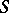 via an order-preserving mapping
via an order-preserving mapping 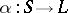 turning
turning 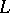 into a glueing with blocks
into a glueing with blocks 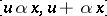 ,
, 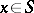 ; this happens if:
; this happens if: 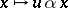 is sup-preserving,
is sup-preserving, 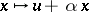 is inf-preserving, and for each
is inf-preserving, and for each  in some generating set there is an
in some generating set there is an 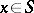 with
with 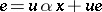 .
.
Every lattice with a tolerance gives rise to a system  of adjunctions between the blocks
of adjunctions between the blocks 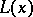 ,
, 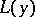 ,
, 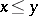 in
in 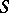 , satisfying certain axioms. Namely,
, satisfying certain axioms. Namely, 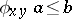 if and only if
if and only if 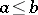 if and only if
if and only if 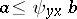 . Conversely, each such system defines a pre-order on the disjoint union of the
. Conversely, each such system defines a pre-order on the disjoint union of the 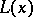 and, factoring by the associated equivalence relation, a lattice with tolerance having blocks
and, factoring by the associated equivalence relation, a lattice with tolerance having blocks 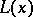 . Glueing always produces a modular lattice from modular blocks, but only in special cases the impact of the Arguesian law and various kinds of representability are understood (a necessary condition is that any pair of adjunctions matching coordinate rings of two frames induces an anti-isomorphism of partially ordered sets [a17]). For the combinatorial analysis of subgroup lattices of finite Abelian groups, cf. [a2].
. Glueing always produces a modular lattice from modular blocks, but only in special cases the impact of the Arguesian law and various kinds of representability are understood (a necessary condition is that any pair of adjunctions matching coordinate rings of two frames induces an anti-isomorphism of partially ordered sets [a17]). For the combinatorial analysis of subgroup lattices of finite Abelian groups, cf. [a2].
Coordinates.
See [a5], [a7]. J. von Neumann introduced the lattice-theoretic analogue of projective coordinate systems: an  -frame consists of independent elements
-frame consists of independent elements 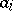 ,
,  ,
, 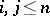 ,
, 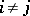 , such that
, such that 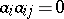 ,
, 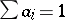 ,
, 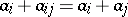 , and
, and 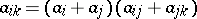 . There are equivalent variants. Any
. There are equivalent variants. Any 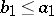 provides frames
provides frames 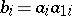 ,
, 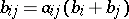 and
and 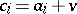 ,
, 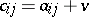 , where
, where 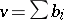 , of sublattices which can be used to derive frames satisfying relations. The elements
, of sublattices which can be used to derive frames satisfying relations. The elements 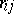 such that
such that 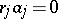 and
and 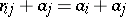 form the coordinate domain
form the coordinate domain 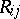 . For a free
. For a free 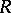 -module with basis
-module with basis 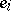 one has the canonical frame
one has the canonical frame 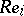 ,
, 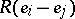 and
and 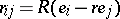 . If
. If 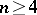 or, in the presence of the Arguesian law,
or, in the presence of the Arguesian law, 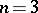 [a6], then the
[a6], then the 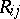 are turned into rings (cf. Ring) isomorphic via
are turned into rings (cf. Ring) isomorphic via 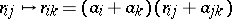 , respectively
, respectively 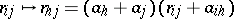 , with unit
, with unit 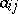 and
and
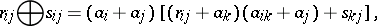 |
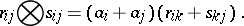 |
Every modular lattice generated by a frame can be generated by 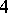 elements. Every finitely-generated semi-group
elements. Every finitely-generated semi-group 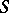 can be embedded into the multiplicative semi-group of the coordinate ring of a suitable frame in some
can be embedded into the multiplicative semi-group of the coordinate ring of a suitable frame in some  -generated sublattice of
-generated sublattice of 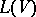 over a given field
over a given field 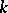 (finite dimensional if
(finite dimensional if 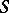 is finite).
is finite).
A complemented Arguesian lattice possessing a large partial  -frame (i.e., a
-frame (i.e., a  -frame of a section
-frame of a section 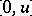 with
with  having a complement
having a complement 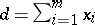 ,
, 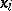 perspective to
perspective to 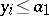 ) or being simple of dimension
) or being simple of dimension 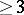 is isomorphic to the lattice of principal right ideals of some regular ring [a23]. Under suitable richness assumptions, lattices
is isomorphic to the lattice of principal right ideals of some regular ring [a23]. Under suitable richness assumptions, lattices 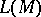 have been characterized for various classes of rings via the Arguesian law and geometric conditions on the lattice, e.g. for completely primary uniserial rings [a24] and left Ore domains. There are results on lattice isomorphisms induced by semi-linear mappings, respectively Morita equivalences (cf. also Morita equivalence), and on lattice homomorphisms induced by tensoring [a1]. Abelian lattices, having certain features of Abelian categories, can be embedded into subgroup lattices of Abelian groups. This includes algebraic modular lattices having an infinite frame [a32].
have been characterized for various classes of rings via the Arguesian law and geometric conditions on the lattice, e.g. for completely primary uniserial rings [a24] and left Ore domains. There are results on lattice isomorphisms induced by semi-linear mappings, respectively Morita equivalences (cf. also Morita equivalence), and on lattice homomorphisms induced by tensoring [a1]. Abelian lattices, having certain features of Abelian categories, can be embedded into subgroup lattices of Abelian groups. This includes algebraic modular lattices having an infinite frame [a32].
Equational theory.
See [a5], [a7], [a8], [a20]. The class of all linear lattices, respectively the class 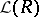 of all lattices embeddable into some
of all lattices embeddable into some  , forms a quasi-variety, since it arises from a projective class in the sense of Mal'tsev. Natural axiom systems and proof theories for quasi-identities have been given, cf. [a10], [a33]. The latter present identities via graphs. On the other hand, there is no finitely-axiomatized quasi-variety containing
, forms a quasi-variety, since it arises from a projective class in the sense of Mal'tsev. Natural axiom systems and proof theories for quasi-identities have been given, cf. [a10], [a33]. The latter present identities via graphs. On the other hand, there is no finitely-axiomatized quasi-variety containing 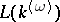 ,
, 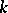 some field, and satisfying all higher-dimensional Arguesian laws. Also, every quasi-variety of modular lattices containing some
some field, and satisfying all higher-dimensional Arguesian laws. Also, every quasi-variety of modular lattices containing some 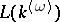 also contains a
also contains a  -generated finitely-presented lattice with unsolvable decision problem for words [a18].
-generated finitely-presented lattice with unsolvable decision problem for words [a18].
Identities are preserved when passing to the ideal lattice; thus, one may assume algebraicity. Frames are projective systems of generators and relations within modular lattices: for each  there are terms
there are terms 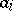 ,
, 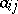 in the variables
in the variables 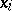 ,
, 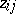 such that the
such that the 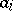 ,
, 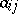 form a frame in a sublattice for any choice of the
form a frame in a sublattice for any choice of the 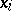 ,
, 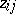 in a modular lattice and
in a modular lattice and  ,
, 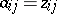 if these happen to form a frame already. This allows one to translate divisibility of integer multiples of
if these happen to form a frame already. This allows one to translate divisibility of integer multiples of 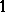 in a ring (more generally, solvability of systems of linear equations with integer coefficients) into lattice identities. The converse has been done in [a19] for lattices of submodules: solving the decision problem for words in free lattices in
in a ring (more generally, solvability of systems of linear equations with integer coefficients) into lattice identities. The converse has been done in [a19] for lattices of submodules: solving the decision problem for words in free lattices in 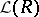 , whenever
, whenever 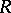 has decidable divisibility of integers (e.g.
has decidable divisibility of integers (e.g. 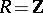 ), and providing a complete list of all varieties
), and providing a complete list of all varieties 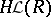 , each generated by finite-dimensional members (related ideas occur in the model theory of modules [a31]). In contrast, no finitely-axiomatized variety of modular lattices containing
, each generated by finite-dimensional members (related ideas occur in the model theory of modules [a31]). In contrast, no finitely-axiomatized variety of modular lattices containing 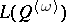 is generated by its finite-dimensional members. For free lattices with
is generated by its finite-dimensional members. For free lattices with 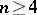 generators in the quasi-varieties of all Arguesian linear, respectively normal, subgroup lattices the decision problem remains open (in contrast to the negative answer for modular lattices [a11]). The corresponding variety containments, with
generators in the quasi-varieties of all Arguesian linear, respectively normal, subgroup lattices the decision problem remains open (in contrast to the negative answer for modular lattices [a11]). The corresponding variety containments, with 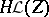 included, are all proper [a25], [a26], [a30]. There are rings
included, are all proper [a25], [a26], [a30]. There are rings 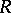 with
with 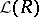 not a variety, but the status for
not a variety, but the status for 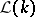 ,
, 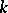 a field,
a field, 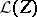 , normal subgroup and linear lattices is unknown. Yet, for finite-dimensional
, normal subgroup and linear lattices is unknown. Yet, for finite-dimensional 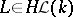 a retraction into
a retraction into 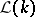 is possible. The variety generated by modular lattices of
is possible. The variety generated by modular lattices of 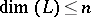 can be finitely axiomatized; for
can be finitely axiomatized; for 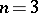 the lattice of subvarieties and the covering varieties have been determined [a20]. Finitely-generated varieties are finitely axiomatizable (this does not extend to quasi-varieties).
the lattice of subvarieties and the covering varieties have been determined [a20]. Finitely-generated varieties are finitely axiomatizable (this does not extend to quasi-varieties).
Generators and relations.
See [a28]. Given a pair 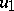 ,
, 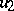 of complements in a modular lattice
of complements in a modular lattice 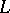 and a subset
and a subset 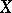 such that
such that 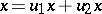 for all
for all 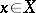 , one has that
, one has that  ,
,  are central in the sublattice they generate together with
are central in the sublattice they generate together with 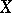 . This applies to a direct decomposition
. This applies to a direct decomposition 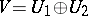 of a representation of a partially ordered set,
of a representation of a partially ordered set, 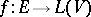 , with
, with 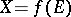 . Hence, for a set
. Hence, for a set 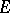 of generators with partial order relation, the subdirectly indecomposable factors of the free lattice in
of generators with partial order relation, the subdirectly indecomposable factors of the free lattice in 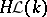 can be obtained via Jónsson's lemma from the subdirectly indecomposable factors of indecomposable finite-dimensional representations. In particular, this carries through for representation-finite
can be obtained via Jónsson's lemma from the subdirectly indecomposable factors of indecomposable finite-dimensional representations. In particular, this carries through for representation-finite 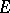 . For
. For 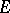 not containing
not containing 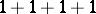 nor
nor 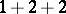 , these are exactly the subdirectly indecomposable modular lattices generated by such
, these are exactly the subdirectly indecomposable modular lattices generated by such 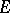 , namely
, namely  - or
- or  -element. For
-element. For  one obtains all
one obtains all 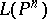 ,
, 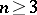 ,
, 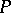 the prime subfield, lattices with
the prime subfield, lattices with 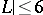 , and a series of
, and a series of  -distributives (with
-distributives (with 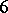 labelings by generators) [a13]. The latter are exactly the subdirectly indecomposable modular lattices generated by two pairs of complements. Also, the structure of the free lattices in
labelings by generators) [a13]. The latter are exactly the subdirectly indecomposable modular lattices generated by two pairs of complements. Also, the structure of the free lattices in 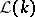 over these and other tame
over these and other tame 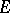 of finite growth is understood [a4]. Moreover, the word problem for
of finite growth is understood [a4]. Moreover, the word problem for 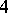 -generated finitely-presented lattices in
-generated finitely-presented lattices in 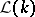 is solvable. The lattice-theoretic approach determines the subdirectly indecomposable factors
is solvable. The lattice-theoretic approach determines the subdirectly indecomposable factors 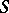 , first, using neutral elements and the splitting method.
, first, using neutral elements and the splitting method.
A large number of finitely-presented modular lattices with additional unary operations have been determined in [a14], [a28] as invariants for the orbits (cf. Orbit) of subspaces under the group of isometric mappings (cf. Isometric mapping) of a vector space endowed with a sesquilinear form. The above methods have been modified to this setting.
The Arguesian lattices generated by a frame can be explicitly determined as certain lattices of subgroups of Abelian groups. To some extent the analysis for  and other generating posets carries over to Arguesian lattices, but essentially new phenomena occur [a15].
and other generating posets carries over to Arguesian lattices, but essentially new phenomena occur [a15].
References
| [a1] | U. Brehm, M. Greferath, S.E. Schmidt, "Projective geometry on modular lattices" F. Buekenhout (ed.) , Handbook of Incidence Geometry , Elsevier (1995) pp. 1115–1142 |
| [a2] | L.M. Butler, "Subgroup lattices and symmetric functions" , Memoirs , 539 , Amer. Math. Soc. (1994) |
| [a3] | P. Crawley, R.P. Dilworth, "Algebraic theory of lattices" , Prentice-Hall (1973) |
| [a4] | A.A. Cylke, "Perfect and linearly equivalent elements in modular lattices" V. Dlab (ed.) etAAsal. (ed.) , Representations of Algebras VI (Proc. Int. Conf. Ottawa 1992) , CMS Conf. Proc. , 14 , Amer. Math. Soc. (1993) pp. 125–148 |
| [a5] | A. Day, "Geometrical applications in modular lattices" R. Freese (ed.) O. Garcia (ed.) , Universal Algebra and Lattice Theory , Lecture Notes in Mathematics , 1004 , Springer (1983) pp. 111–141 |
| [a6] | A. Day, D. Pickering, "The coordinatization of Arguesian lattices" Trans. Amer. Math. Soc. , 278 (1983) pp. 507–522 |
| [a7] | A. Day, "Applications of coordinatization in modular lattice theory: the legacy of J. von Neumann" Order , 1 (1985) pp. 295–300 |
| [a8] | A. Day, R. Freese, "The role of gluing in modular lattice theory" K. Bogart (ed.) R. Freese (ed.) J. Kung (ed.) , The Dilworth Theorems, Selected Papers of Robert P. Dilworth , Birkhäuser (1990) pp. 251–260 |
| [a9] | H. (eds.) Draškovičová, etAAsal., "Ordered sets and lattices, I--II" Amer. Math. Soc. Transl. Ser. 2 , 142, 152 (1989/1992) |
| [a10] | D. Finberg, M. Mainetti, G.-C. Rota, "The logic of computing with equivalence relations" A. Ursini (ed.) P. Agliano (ed.) , Logic and Algebra , Lecture Notes Pure Applied Math. , 180 , M. Dekker (1996) |
| [a11] | R. Freese, "Free modular lattices" Trans. Amer. Math. Soc. , 261 (1980) pp. 81–91 |
| [a12] | R. Freese, R. McKenzie, "Commutator theory for congruence modular varieties" , Lecture Notes , 125 , London Math. Soc. (1987) |
| [a13] | "Representation theory. Selected papers" I.M. Gel'fand (ed.) , Lecture Notes , 69 , London Math. Soc. (1982) |
| [a14] | H. Gross, "Quadratic forms in infinite dimensional vector spaces" , Progress in Math. , 1 , Birkhäuser (1979) |
| [a15] | C. Herrmann, "On elementary Arguesian lattices with four generators" Algebra Universalis , 18 (1984) pp. 225–259 |
| [a16] | C. Herrmann, D. Pickering, M. Roddy, "Geometric description of modular lattices" Algebra Universalis , 31 (1994) pp. 365–396 |
| [a17] | C. Herrmann, "Alan Day's work on modular and Arguesian lattices" Algebra Universalis , 34 (1995) pp. 35–60 |
| [a18] | G. Hutchinson, "Embedding and unsolvability theorems for modular lattices" Algebra Universalis , 7 (1977) pp. 47–84 |
| [a19] | G. Hutchinson, G. Czédli, "A test for identities satisfied in lattices of submodules" Algebra Universalis , 8 (1978) pp. 269–309 |
| [a20] | P. Jipsen, H. Rose, "Varieties of lattices" , Lecture Notes in Mathematics , 1533 , Springer (1992) |
| [a21] | B. Jónsson, "On the representation of lattices" Math. Scand. , 1 (1953) pp. 193–206 |
| [a22] | B. Jónsson, "Modular lattices and Desargues' theorem" Math. Scand. , 2 (1954) pp. 295–314 |
| [a23] | B. Jónsson, "Representations of complemented modular lattices" Trans. Amer. Math. Soc. , 60 (1960) pp. 64–94 |
| [a24] | B. Jónsson, G. Monk, "Representation of primary Arguesian lattices" Pacific J. Math. , 30 (1969) pp. 95–130 |
| [a25] | B. Jónsson, "Varieties of algebras and their congruence varieties" , Proc. Int. Congress Math., Vancouver (1974) pp. 315–320 |
| [a26] | B. Jónsson, "Congruence varieties" , G. Grätzer: Universal Algebra , Springer (1978) pp. 348–377 (Appendix 3) |
| [a27] | R. McKenzie, G. McNulty, W. Taylor, "Algebras, lattices, varieties" , I , Wadsworth (1987) |
| [a28] | "Orthogonal geometry in infinite dimensional vector spaces" H.A. Keller (ed.) U.-M. Kuenzi (ed.) H. Storrer (ed.) M. Wild (ed.) , Lecture Notes in Mathematics , Springer (to appear) |
| [a29] | C. Năstăsecu, F. van Ostayen, "Dimensions of ring theory" , Reidel (1987) |
| [a30] | P.P. Pálfy, C. Szabó, "Congruence varieties of groups and Abelian groups" K. Baker (ed.) R. Wille (ed.) , Lattice Theory and Its Applications , Heldermann (1995) |
| [a31] | M. Prest, "Model theory and modules" , Lecture Notes , 130 , London Math. Soc. (1988) |
| [a32] | G. Hutchinson, "Modular lattices and abelian categories" J. Algebra , 19 (1971) pp. 156–184 |
| [a33] | G. Hutchinson, "On the representation of lattices by modules" Trans. Amer. Math. Soc. , 209 (1975) pp. 47–84 |
Arguesian lattice. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Arguesian_lattice&oldid=13684