Hilbert geometry
The geometry of a complete metric space 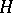 with a metric
with a metric 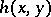 which contains, together with two arbitrary, distinct points
which contains, together with two arbitrary, distinct points  and
and 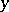 , also the points
, also the points  and
and 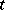 for which
for which 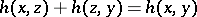 ,
, 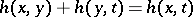 , and which is homeomorphic to a convex set in an
, and which is homeomorphic to a convex set in an  -dimensional affine space
-dimensional affine space 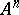 , the geodesics
, the geodesics 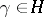 being mapped to straight lines of
being mapped to straight lines of 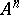 . Thus, let
. Thus, let 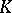 be a convex body in
be a convex body in 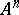 with boundary
with boundary 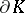 not containing two non-collinear segments, and let
not containing two non-collinear segments, and let 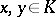 be located on a straight line
be located on a straight line 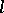 which intersects
which intersects 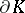 at
at  and
and 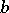 ; let
; let 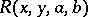 be the cross ratio of
be the cross ratio of  ,
, 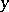 ,
,  ,
, 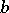 (so that if
(so that if 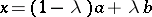 ,
, 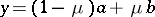 , then
, then 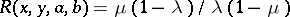 ). Then
). Then
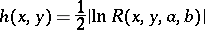 |
is the metric of a Hilbert geometry (a Hilbert metric). If 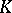 is centrally symmetric, then
is centrally symmetric, then 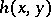 is a Minkowski metric (cf. Minkowski geometry); if
is a Minkowski metric (cf. Minkowski geometry); if 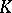 is an ellipsoid, then
is an ellipsoid, then 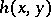 defines the Lobachevskii geometry.
defines the Lobachevskii geometry.
The problem of determining all metrizations of  for which the geodesics are straight lines is Hilbert's fourth problem; it has been completely solved [4].
for which the geodesics are straight lines is Hilbert's fourth problem; it has been completely solved [4].
Geodesic geometry is a generalization of Hilbert geometry.
Hilbert geometry was first mentioned in 1894 by D. Hilbert in a letter to F. Klein.
References
| [1] | D. Hilbert, "Grundlagen der Geometrie" , Springer (1913) |
| [2] | "Hilbert problems" Bull. Amer. Math. Soc. , 8 (1902) pp. 437–479 (Translated from German) |
| [3] | H. Busemann, "The geometry of geodesics" , Acad. Press (1955) |
| [4] | A.V. Pogorelov, "Hilbert's fourth problem" , Winston & Wiley (1974) (In Russian) |
Comments
References
| [a1] | H. Busemann, P.J. Kelly, "Projective geometry and projective metrics" , Acad. Press (1953) |
| [a2] | M. Berger, "Geometry" , I , Springer (1987) |
Hilbert geometry. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hilbert_geometry&oldid=13680