Shadow space

of a Tits building

Let be a Tits building. Denote its index set by . A facet of this building is a simplex. Suppose 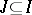is the type of this simplex. A facet corresponds bijectively to the connected component of a chamber containing in the graph whose vertices are the chambers of and in which two chambers are adjacent if and only if they are 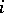-adjacent for some 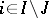. Facets can be used to describe the intuitively known geometries related to buildings. Such geometries are known as shadow spaces of the building, and are made up of the point set 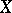of all facets of a given type 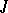, and a distinguished collection 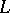of subsets of 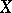. 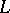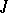A member of is called a line, and consists of all the points (simplices of type ) such that 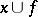is a chamber, for a given simplex of type 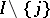for some 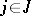(in which case the line is also called a -line). In most cases of interest, and so there is only one type of line. The result is called the shadow space over .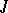

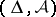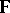For example, if is the building corresponding to projective space of rank over the field , then its index set is 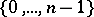. If 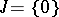, then the shadow space over 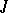is the usual projective space, in the sense that points and lines of the shadow space correspond to the usual projective points and projective lines of the projectivized space of 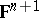. 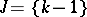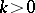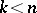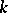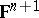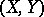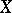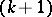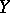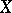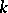More generally, if for some , , the shadow space is the Grassmannian geometry whose points are the -dimensional linear subspaces of , and in which lines are parametrized by pairs consisting of a -dimensional subspace and a -dimensional subspace containing , in such a way that the line corresponding to is the set of all -dimensional linear subspaces 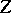of with .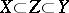

The classical Veblen–Young theorem (cf. [a1]) gives axiomatic conditions for a set of points and lines to be a shadow space over 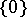of the building of a projective space. Characterization theorems for Grassmannian geometries are known as well, see [a2].

Polar spaces are shadow spaces of type 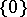of buildings of type 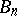, , 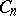or 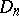. Here, two distinct points are on at most one line. Their main characteristic property is: for each line 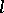and each point 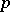either one line through 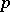is concurrent with 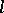(and so exactly one point of 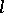is collinear with 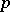) or each point of 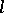is collinear with 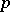. By results of F. Buekenhout, E. Shult, J. Tits, and F. Veldkamp, this property and some non-degeneracy conditions suffice to characterize polar spaces.

Characterizations of more general shadow spaces are surveyed in [a1].

References

[a1]	"The Handbook of Incidence Geometry, Buildings and Foundations" F. Buekenhout (ed.) , Elsevier (1995)
[a2]	A.M. Cohen, "On a theorem of Cooperstein" European J. Combin. , 4 (1983) pp. 107–126