Connections on a manifold
Differential-geometric structures (cf. Differential-geometric structure) on a smooth manifold  that are connections (cf. Connection) on smooth fibre bundles
that are connections (cf. Connection) on smooth fibre bundles  with homogeneous spaces
with homogeneous spaces  of the same dimension as
of the same dimension as  as typical fibres over the base
as typical fibres over the base  . Depending on the choice of the homogeneous space
. Depending on the choice of the homogeneous space  one obtains, for example, affine, projective, conformal, etc., connections on
one obtains, for example, affine, projective, conformal, etc., connections on  (cf. Affine connection; Conformal connection; Projective connection). The general notion of a connection on a manifold was introduced by E. Cartan [1], who called a manifold
(cf. Affine connection; Conformal connection; Projective connection). The general notion of a connection on a manifold was introduced by E. Cartan [1], who called a manifold  with a connection defined on it a "non-holonomic space with a fundamental groupnon-holonomic space with a fundamental group" .
with a connection defined on it a "non-holonomic space with a fundamental groupnon-holonomic space with a fundamental group" .
The modern definition of a connection on a manifold  is based on the concept of a smooth fibre bundle over the base
is based on the concept of a smooth fibre bundle over the base 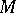 . Let
. Let  be a homogeneous space of the same dimension as
be a homogeneous space of the same dimension as  (for example, an affine space, a projective space, etc.). Let
(for example, an affine space, a projective space, etc.). Let 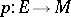 be a smooth locally trivial fibration with typical fibre
be a smooth locally trivial fibration with typical fibre 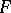 and suppose that in this fibration there is fixed a smooth section
and suppose that in this fibration there is fixed a smooth section  , that is, a smooth mapping
, that is, a smooth mapping  such that
such that  for every
for every 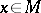 . The last condition ensures that
. The last condition ensures that  is a diffeomorphism of
is a diffeomorphism of  onto
onto 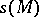 , and therefore
, and therefore 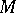 and
and 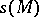 can be identified, if desired. In other words, to each point
can be identified, if desired. In other words, to each point 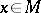 there is associated a copy
there is associated a copy  of the homogeneous space
of the homogeneous space 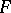 of the same dimension as
of the same dimension as  (that is, the fibre of
(that is, the fibre of 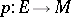 over
over  ) with a fixed point
) with a fixed point 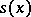 that can be identified with
that can be identified with  .
.
A connection on a manifold is a special case of the more general concept of a connection; it can be defined independently as follows. Suppose that for each piecewise-smooth curve 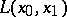 on a manifold
on a manifold  there is an isomorphism
there is an isomorphism  of the tangent homogeneous spaces at the end points of the curve (for example, if
of the tangent homogeneous spaces at the end points of the curve (for example, if  is an affine or projective space, then
is an affine or projective space, then 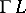 is, respectively, an affine or projective mapping). In addition, suppose that
is, respectively, an affine or projective mapping). In addition, suppose that
1) for 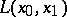 ,
, 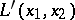 ,
, 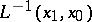 , and
, and  one has
one has  ,
, 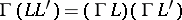 ;
;
2) for each point 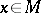 and for each tangent vector
and for each tangent vector 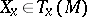 the isomorphism
the isomorphism 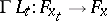 , where
, where  denotes the image of
denotes the image of  under the parametrization
under the parametrization 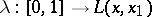 of
of  with tangent vector
with tangent vector 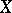 , tends to the identity isomorphism as
, tends to the identity isomorphism as 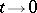 , and its deviation from the latter depends in its principal part only on
, and its deviation from the latter depends in its principal part only on  and
and  , and this dependence is smooth.
, and this dependence is smooth.
In this case it is said that a connection 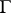 of type
of type  is defined on
is defined on  ; the isomorphism
; the isomorphism 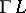 is called the parallel displacement along
is called the parallel displacement along 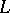 . For each curve
. For each curve 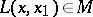 its evolute is defined, that is, the curve in
its evolute is defined, that is, the curve in  that consists of the image of the points
that consists of the image of the points 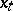 of
of 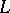 under parallel displacement along
under parallel displacement along 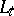 . It follows from 2) that curves with common tangent vector
. It follows from 2) that curves with common tangent vector  at a point
at a point  have evolutes with common tangent vector
have evolutes with common tangent vector  that depends smoothly on
that depends smoothly on  and
and 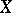 . A consequence of this is that for each point
. A consequence of this is that for each point  there is a mapping
there is a mapping
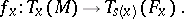 |
The connections on a manifold that have been studied most are linear connections, which have the following additional property:
3) the element 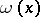 in the Lie algebra
in the Lie algebra  of the structure group
of the structure group  that defines the principal part of the deviation of the isomorphism
that defines the principal part of the deviation of the isomorphism 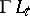 from the identity isomorphism as
from the identity isomorphism as  relative to a certain field of frames, depends linearly on
relative to a certain field of frames, depends linearly on  .
.
In this case  is a linear mapping. If
is a linear mapping. If 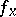 is an isomorphism for any point
is an isomorphism for any point  , then one speaks about a non-degenerate connection on a manifold, or about a Cartan connection; in this case the isomorphism
, then one speaks about a non-degenerate connection on a manifold, or about a Cartan connection; in this case the isomorphism 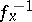 is also treated as a glueing of the fibration
is also treated as a glueing of the fibration 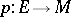 to the base
to the base 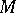 (along a given section
(along a given section  ). A Cartan connection on
). A Cartan connection on 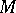 is called complete if for each point
is called complete if for each point  , any smooth curve in
, any smooth curve in  that begins at
that begins at  is the evolute of a curve on
is the evolute of a curve on  .
.
There is another point of view of the general theory of connections, where a linear connection in the fibration 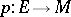 is defined by using a horizontal distribution
is defined by using a horizontal distribution 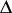 on
on 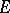 . Then the mapping
. Then the mapping  is the composite of an isomorphism
is the composite of an isomorphism 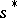 that maps
that maps  into the corresponding tangent vector to
into the corresponding tangent vector to  , followed by a projection of the space
, followed by a projection of the space 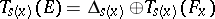 onto the second direct summand. Hence it follows that a connection is non-degenerate if and only if
onto the second direct summand. Hence it follows that a connection is non-degenerate if and only if  for any
for any 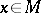 . To
. To  all concepts and results developed in the general theory of connections can be applied. Such are, e.g., the holonomy group, the curvature form, the holonomy theorem, etc. The additional structure of a fibre bundle over the manifold
all concepts and results developed in the general theory of connections can be applied. Such are, e.g., the holonomy group, the curvature form, the holonomy theorem, etc. The additional structure of a fibre bundle over the manifold  enables one, however, to introduce certain more special concepts. Apart from evolutes, the most most important of these is the concept of the torsion form of a connection on
enables one, however, to introduce certain more special concepts. Apart from evolutes, the most most important of these is the concept of the torsion form of a connection on 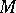 at
at  .
.
The Cartan connections in the case when 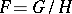 is a homogeneous reductive space (that is, when there is a direct decomposition
is a homogeneous reductive space (that is, when there is a direct decomposition 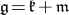 with the property
with the property 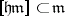 ) occupy a special position in the theory of connections on a manifold. In this case the curvature form
) occupy a special position in the theory of connections on a manifold. In this case the curvature form  splits into two independent objects: its component in
splits into two independent objects: its component in 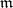 generates the torsion form, and the component in
generates the torsion form, and the component in 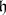 generates the curvature form. The best-known example here is an affine connection on
generates the curvature form. The best-known example here is an affine connection on 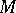 for which
for which 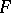 is an affine space of the same dimension as
is an affine space of the same dimension as 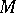 .
.
A reductive space 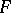 has an invariant affine connection. More generally, if there is an invariant affine or projective connection on
has an invariant affine connection. More generally, if there is an invariant affine or projective connection on 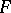 , then the geodesic lines (cf. Geodesic line) of a connection of type
, then the geodesic lines (cf. Geodesic line) of a connection of type 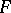 are defined on
are defined on 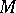 as those lines possessing evolutes which are geodesic lines of the given invariant connection.
as those lines possessing evolutes which are geodesic lines of the given invariant connection.
References
| [1] | E. Cartan, "Espaces à connexion affine, projective et conforme" Acta Math. , 48 (1926) pp. 1–42 |
| [2] | G.F. Laptev, "Differential geometry of imbedded manifolds. Group-theoretical method of differential-geometric investigations" Trudy Moskov. Mat. Obshch. , 2 (1953) pp. 275–382 (In Russian) |
| [3] | Ch. Ehresmann, "Les connexions infinitésimal dans une espace fibré différentiable" , Colloq. de Topologie Bruxelles, 1950 , G. Thone & Masson (1951) pp. 29–55 |
| [4] | S. Kobayashi, "On connections of Cartan" Canad. J. Math. , 8 : 2 (1956) pp. 145–156 |
| [5] | Y.H. Clifton, "On the completeness of Cartan connections" J. Math. Mech. , 16 : 6 (1966) pp. 569–576 |
Comments
Let 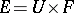 be a trivial vector bundle. The principal part of an element
be a trivial vector bundle. The principal part of an element 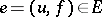 is the component
is the component  . Similarly, if
. Similarly, if 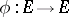 is a bundle homomorphism (
is a bundle homomorphism (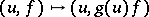 ), then
), then 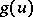 , or
, or 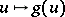 , is its principal part. See also the editorial comments to Connection.
, is its principal part. See also the editorial comments to Connection.
Connections on a manifold. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Connections_on_a_manifold&oldid=13655