Multiplier group
From Encyclopedia of Mathematics
multiplicator, of a group 
represented as a quotient group 
of a free group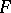 
The quotient group
 |
where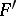 
is the commutator subgroup of 
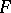and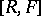 
is the mutual commutator subgroup of 
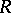and 
. The multiplicator of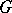 
does not depend on the way in which 
is presented as a quotient group of a free group. It is isomorphic to the second homology group of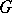 
with integer coefficients. In certain branches of group theory the question of non-triviality of the multiplicator of a group is important.
Comments
The usual name in the Western literature is Schur multiplier (or multiplicator). It specifically enters in the study of central extensions of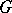 
and in the study of perfect groups 
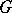(i.e. groups 
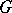for which 
, where 
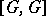is the commutator subgroup of 
).
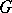References
| [a1] | D.J.S. Robinson, "A course in the theory of groups" , Springer (1980) |
How to Cite This Entry:
Multiplier group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Multiplier_group&oldid=13653
Multiplier group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Multiplier_group&oldid=13653
This article was adapted from an original article by A.L. Shmel'kin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article