Pontryagin number
A characteristic number defined for closed oriented manifolds and assuming rational values. Let  be an arbitrary (not necessarily homogeneous) stable characteristic class. For a closed oriented manifold
be an arbitrary (not necessarily homogeneous) stable characteristic class. For a closed oriented manifold 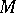 the rational number
the rational number 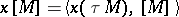 is called the Pontryagin number of
is called the Pontryagin number of  corresponding to
corresponding to  ; here
; here  is the tangent bundle and
is the tangent bundle and  is the fundamental class of
is the fundamental class of 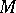 . The Pontryagin number
. The Pontryagin number  depends only on the homogeneous component of degree
depends only on the homogeneous component of degree 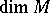 of the class
of the class  . Let
. Let 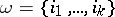 be a partition of
be a partition of  , i.e. a set of non-negative integers
, i.e. a set of non-negative integers 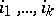 such that
such that 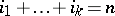 and let
and let 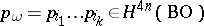 . The rational numbers
. The rational numbers 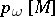 are defined for a closed manifold
are defined for a closed manifold 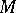 of dimension
of dimension 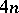 and all partitions
and all partitions 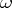 of the number
of the number  .
.
The Pontryagin numbers 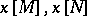 of two bordant (in the oriented sense, cf. Bordism) manifolds
of two bordant (in the oriented sense, cf. Bordism) manifolds 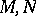 are equal:
are equal:  (Pontryagin's theorem).
(Pontryagin's theorem).
According to this theorem each characteristic class 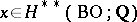 induces a homomorphism
induces a homomorphism 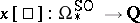 , and each element
, and each element 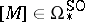 induces a homomorphism
induces a homomorphism 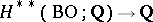 ,
, 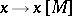 . In other words, there is a mapping
. In other words, there is a mapping
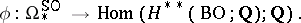 |
If all Pontryagin numbers and Stiefel numbers (cf. Stiefel number) of two oriented closed manifolds coincide, then these manifolds are bordant (in the oriented sense).
A problem similar to the Milnor–Hirzebruch problem for quasi-complex manifolds consists in describing the image of the mapping 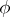 . The solution of this problem is based on the consideration of Pontryagin numbers in
. The solution of this problem is based on the consideration of Pontryagin numbers in 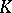 -theory corresponding to the Pontryagin classes (cf. Pontryagin class)
-theory corresponding to the Pontryagin classes (cf. Pontryagin class) 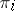 in
in 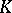 -theory. Let
-theory. Let 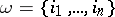 be a set of non-negative integers, let
be a set of non-negative integers, let 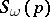 and
and 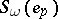 be the characteristic classes defined by the symmetric series
be the characteristic classes defined by the symmetric series
 |
respectively; here 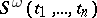 is the minimal symmetric polynomial containing the monomials
is the minimal symmetric polynomial containing the monomials 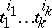 ,
, 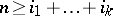 . Let
. Let 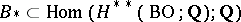 be a set of homomorphisms
be a set of homomorphisms  for which
for which 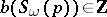 ,
, 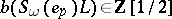 for all tuples
for all tuples 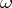 . Then the image of the homomorphism
. Then the image of the homomorphism
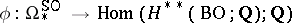 |
coincides with 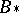 (the Stong–Hattori theorem).
(the Stong–Hattori theorem).
The characteristic numbers  and
and  corresponding to the classes
corresponding to the classes  are called the
are called the 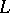 -genus and the
-genus and the 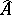 -genus of
-genus of 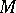 , respectively.
, respectively.
For a closed manifold 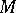 of dimension divisible by
of dimension divisible by 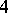 the equality
the equality 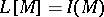 holds, where
holds, where 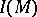 is the signature of the manifold, i.e. the signature of the quadratic intersection form defined on
is the signature of the manifold, i.e. the signature of the quadratic intersection form defined on 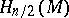 ,
,  (Hirzebruch's theorem). For a closed spin manifold
(Hirzebruch's theorem). For a closed spin manifold 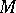 of even dimension the spinor index of
of even dimension the spinor index of 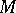 , i.e. the index of the Dirac operator on
, i.e. the index of the Dirac operator on 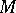 , coincides with
, coincides with 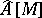 .
.
For references see Pontryagin class.
Pontryagin number. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pontryagin_number&oldid=13650