Extension of a group
A group containing the given group as a normal subgroup. The quotient group is usually prescribed as well, that is, an extension of a group 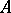 by a group
by a group  is a group
is a group  containing
containing  as a normal subgroup and such that
as a normal subgroup and such that  , i.e. it is an exact sequence
, i.e. it is an exact sequence
 | (1) |
In the literature other terminology is sometimes adopted, e.g.,  may be called an extension of
may be called an extension of 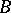 by
by  (see [2], for example), the epimorphism
(see [2], for example), the epimorphism 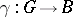 itself may be called an extension of
itself may be called an extension of 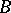 (see [1]), or the exact sequence (1) may be called an extension of
(see [1]), or the exact sequence (1) may be called an extension of 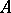 by
by 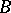 , or an extension of
, or an extension of 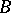 by
by 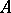 . An extension of
. An extension of 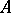 by
by 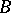 always exists, although it is not uniquely determined by
always exists, although it is not uniquely determined by  and
and 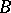 . The need to describe all extensions of
. The need to describe all extensions of 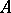 by
by  up to a natural equivalence is motivated by the demands both of group theory itself and of its applications. Two extensions of
up to a natural equivalence is motivated by the demands both of group theory itself and of its applications. Two extensions of 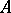 by
by 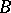 are called equivalent if there is a commutative diagram
are called equivalent if there is a commutative diagram
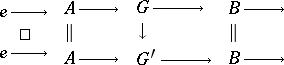 |
Any extension of the form (1) determines, via conjugation of the elements of the group 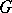 , a homomorphism
, a homomorphism 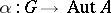 , where
, where 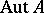 is the automorphism group of
is the automorphism group of 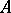 ,
,
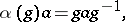 |
such that 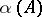 is contained in the group
is contained in the group 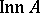 of inner automorphisms of
of inner automorphisms of 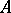 . Hence
. Hence 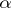 induces a homomorphism
induces a homomorphism
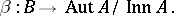 |
The triple 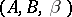 is called the abstract kernel of the extension. Given an extension (1), one chooses for every
is called the abstract kernel of the extension. Given an extension (1), one chooses for every 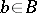 a representative
a representative 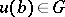 in such a way that
in such a way that  and
and  . Then conjugation by
. Then conjugation by 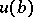 determines an automorphism
determines an automorphism 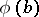 of
of 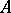 ,
,
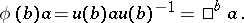 |
The product of 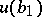 and
and  is equal to
is equal to 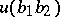 up to a factor
up to a factor 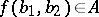 :
:
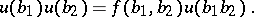 |
It is easily checked that these functions must satisfy the conditions
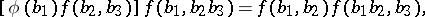 | (2) |
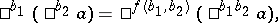 | (3) |
where the function 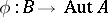 is implicit in (3).
is implicit in (3).
Given groups 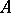 and
and 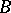 and functions
and functions  ,
, 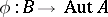 satisfying (2), (3) and the normalization conditions
satisfying (2), (3) and the normalization conditions
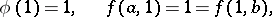 |
one can define an extension (1) in the following way. The product set 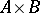 is a group under the operation
is a group under the operation
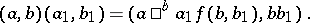 |
The homomorphisms 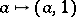 ,
, 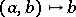 yield an extension.
yield an extension.
Given an abstract kernel 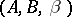 , it is always possible to find a normalized function
, it is always possible to find a normalized function 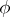 satisfying condition (3). A function
satisfying condition (3). A function 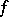 arises naturally, but condition (2) is not always fulfilled. In general,
arises naturally, but condition (2) is not always fulfilled. In general,
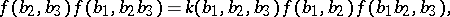 |
where 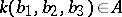 . The function
. The function 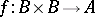 is called a factor set and
is called a factor set and 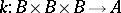 is called the obstruction to the extension. If the group
is called the obstruction to the extension. If the group 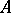 is Abelian, then the factor sets form a group
is Abelian, then the factor sets form a group 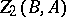 under natural composition. Factor sets corresponding to a semi-direct product form a subgroup
under natural composition. Factor sets corresponding to a semi-direct product form a subgroup 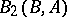 of
of 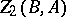 . The quotient group
. The quotient group 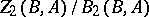 is isomorphic to the second cohomology group of
is isomorphic to the second cohomology group of 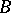 with coefficients in
with coefficients in 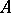 . Obstructions have a similar interpretation in the third cohomology group.
. Obstructions have a similar interpretation in the third cohomology group.
The idea of studying extensions by means of factor sets appeared long ago (O. Hölder, 1893). However, the introduction of factor sets is usually connected with the name of O. Schreier, who used them to undertake the first systematic study of extensions. R. Baer was the first to carry out an invariant study of group extensions without using factor sets. The theory of group extensions is one of the cornerstones of homological algebra.
References
| [1] | H. Cartan, S. Eilenberg, "Homological algebra" , Princeton Univ. Press (1956) |
| [2] | A.A. Kirillov, "Elements of the theory of representations" , Springer (1976) (Translated from Russian) |
| [3] | A.G. Kurosh, "The theory of groups" , 1–2 , Chelsea (1955–1956) (Translated from Russian) |
| [4] | S. MacLane, "Homology" , Springer (1963) |
Comments
References
| [a1] | S. Eilenberg, S. MacLane, "Cohomology theory in abstract groups II" Ann. of Math. , 48 (1947) pp. 326–341 |
Extension of a group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Extension_of_a_group&oldid=13641