Markov spectrum problem

A problem in number theory which arises in connection with the distribution of the normalized values of arithmetic minima of indefinite binary quadratic forms (cf. Binary quadratic form). Let

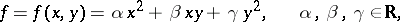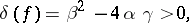and let

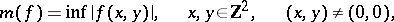be the uniform arithmetic minimum of the form 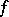. The number

is called the Markov constant of 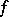. The set 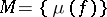, where runs through all real indefinite quadratic forms, is called the Markov spectrum. The Markov constant and the Markov spectrum have been defined in various ways; in particular, A.A. Markov in

considered the set 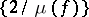. It is known that 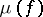is an invariant of a ray of classes of forms, that is, of a set

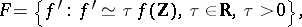(1)

since 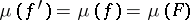. Each ray of classes 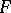is in one-to-one correspondence with a doubly-infinite (infinite in both directions) sequence

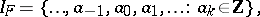such that if one puts

( is the notation for a continued fraction), then

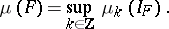The Markov problem can be stated as follows: 1) describe the Markov spectrum 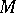; and 2) for each , describe the set of forms 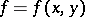(or the rays 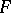) for which 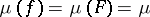. The problem was solved by Markov for the initial part of the spectrum defined by the condition 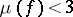. This part of the spectrum is a discrete set:

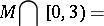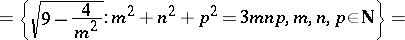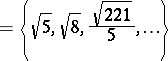with the unique limit point 3 (a condensation point of ); , and run through all positive integer solutions of Markov's Diophantine equation

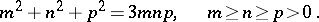(2)

In this case there corresponds to each point of this part of the spectrum precisely one ray 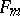, given by a Markov form , with

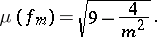A solution 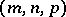of (2) is called a Markov triple; the number 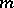is called a Markov number. The Markov form 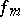is associated to the Markov number as follows. Let be defined by the conditions

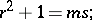then, by definition,

The set 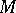is closed and there is a smallest number 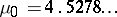such that 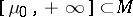and borders the interval of contiguity of .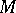

The Markov problem is closely related to the Lagrange–Hurwitz problem on rational approximation of a real number 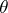. The quantity

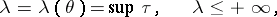where the least upper bound is taken over all , , 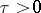for which

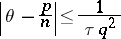has an infinite set of solutions , , 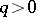is called a Lagrange constant. The set 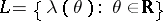is called the Lagrange spectrum. It is natural to regard Lagrange's theorem as the first result in the theory of the Lagrange spectrum: All convergents of the continued fraction expansion of 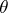satisfy

If 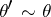, that is, if

then 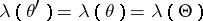, where 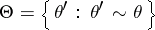is an equivalence class of numbers. If 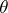is expanded as a continued fraction 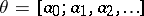, then

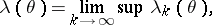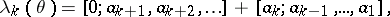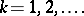Thus, the Lagrange–Hurwitz problem can be stated as: a) describe the Lagrange spectrum 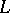; and b) for each 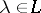, describe the set of numbers 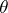(or classes 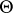) for which .

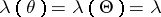For this problem reduces to the Markov problem; moreover,

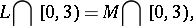and to each , , 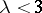corresponds precisely one class 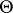, described by the Markov form 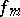, provided the unicity conjecture is true. It has been proved that 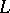, like 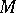, is a closed set; tha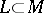t but 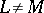; that

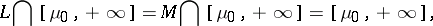where borders the interval of contiguity of 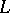. Research into the structure of 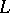and the connection between 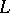and 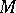is described in [6]. For generalizations and analogues of the Markov spectrum problem and "isolation phenomena" see [2], [3], [7].

References

[1a]	A. [A.A. Markov] Markoff, "Sur les formes quadratiques binaires indéfinies" Math. Ann. , 15 (1879) pp. 381–406
[1b]	A. [A.A. Markov] Markoff, "Sur les formes quadratiques binaires indéfinies" Math. Ann. , 17 (1880) pp. 379–400
[2]	J.W.S. Cassels, "An introduction to diophantine approximation" , Cambridge Univ. Press (1957)
[3]	B.N. Delone, "The Peterburg school of number theory" , Moscow-Leningrad (1947) (In Russian)
[4]	D.S. Gorshkov, "Lobachevskii geometry in connection with some problems of arithmetic" Zap. Nauchn. Sem. Leningrad. Otdel. Mat. Inst. Steklov. , 67 (1977) pp. 39–85 (In Russian)
[5]	G.A. Freiman, "Diophantine approximation and the geometry of numbers. (The Markov problem)" , Kalinin (1975) (In Russian)
[6]	A.V. Malyshev, "Markov and Lagrange spectra (a survey of the literature)" Zap. Nauchn. Sem. Leningrad. Otdel. Mat. Inst. Steklov. , 67 (1977) pp. 5–38 (In Russian)
[7]	B.A. Venkov, "On an extremum problem of Markov for indefinite ternaire quadratic forms" Izv. Akad. Nauk SSSR Ser. Mat. , 9 (1945) pp. 429–494 (In Russian) (French summary)

Comments

In equation (1) in the article above, the notation 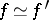(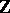) refers to equivalence of binary forms over 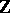. More precisely, 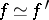(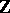) if and only if there are integers , such that .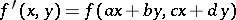

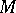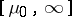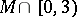The "interval of contiguity of a Markov spectruminterval of contiguity" of is simply the maximal interval completely belonging to . The intersections and 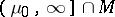have been well-described. The structure of the portion between, i.e. 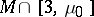, is still (1989) unclear.

The unicity conjecture claims that the Markov number 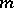uniquely determines the triplet (and thus the Markov form 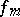). It is still (1989) a conjecture.

References

[a1]	D. Zagier, "On the number of Markoff numbers below a given bound" Math. Comp. , 39 (1982) pp. 709–723
[a2]	T.W. Cusick, M.E. Flahive, "The Markoff and Lagrange spectra" , Amer. Math. Soc. (1989)