Integrating factor
of an ordinary first-order differential equation
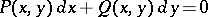 |
A function  with the property that
with the property that
 |
is a differential equation with total differential. E.g., for the linear equation 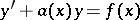 , or
, or 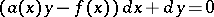 , the function
, the function  is an integrating factor. If in a domain
is an integrating factor. If in a domain 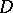 where
where  equation
equation
has a smooth general integral 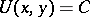 , then it has an infinite number of integrating factors. If
, then it has an infinite number of integrating factors. If 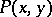 and
and  have continuous partial derivatives in a domain
have continuous partial derivatives in a domain  where
where 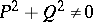 , then any particular (non-trivial) solution of the partial differential equation
, then any particular (non-trivial) solution of the partial differential equation
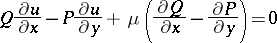 | (2) |
can be taken as integrating factor, see [1]. However, a general method for finding solutions of (2) does not exist, and hence it is only in exceptional cases that one succeeds in finding an integrating factor for a concrete equation , cf. [2].
References
| [1] | W.W. [V.V. Stepanov] Stepanow, "Lehrbuch der Differentialgleichungen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian) |
| [2] | E. Kamke, "Differentialgleichungen: Lösungen und Lösungsmethoden" , 1. Gewöhnliche Differentialgleichungen , Chelsea, reprint (1971) |
Integrating factor. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Integrating_factor&oldid=13624