Plurisubharmonic function
A real-valued function 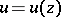 ,
, 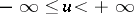 , of
, of  complex variables
complex variables 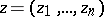 in a domain
in a domain 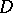 of the complex space
of the complex space 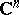 ,
, 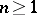 , that satisfies the following conditions: 1)
, that satisfies the following conditions: 1) 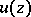 is upper semi-continuous (cf. Semi-continuous function) everywhere in
is upper semi-continuous (cf. Semi-continuous function) everywhere in 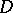 ; and 2)
; and 2) 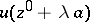 is a subharmonic function of the variable
is a subharmonic function of the variable 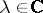 in each connected component of the open set
in each connected component of the open set 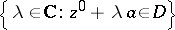 for any fixed points
for any fixed points 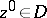 ,
, 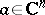 . A function
. A function 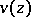 is called a plurisuperharmonic function if
is called a plurisuperharmonic function if 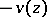 is plurisubharmonic. The plurisubharmonic functions for
is plurisubharmonic. The plurisubharmonic functions for 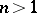 constitute a proper subclass of the class of subharmonic functions, while these two classes coincide for
constitute a proper subclass of the class of subharmonic functions, while these two classes coincide for 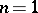 . The most important examples of plurisubharmonic functions are
. The most important examples of plurisubharmonic functions are 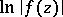 ,
, 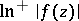 ,
, 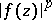 ,
, 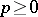 , where
, where 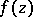 is a holomorphic function in
is a holomorphic function in 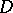 .
.
For an upper semi-continuous function 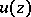 ,
, 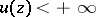 , to be plurisubharmonic in a domain
, to be plurisubharmonic in a domain 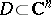 , it is necessary and sufficient that for every fixed
, it is necessary and sufficient that for every fixed 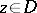 ,
, 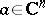 ,
,  , there exists a number
, there exists a number 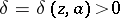 such that the following inequality holds for
such that the following inequality holds for 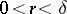 :
:
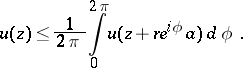 |
The following criterion is more convenient for functions 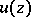 of class
of class 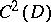 :
: 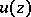 is a plurisubharmonic function in
is a plurisubharmonic function in 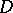 if and only if the Hermitian form (the Hessian of
if and only if the Hermitian form (the Hessian of  , cf. Hessian of a function)
, cf. Hessian of a function)
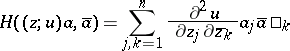 |
is positive semi-definite at each point 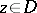 .
.
The following hold for plurisubharmonic functions, in addition to the general properties of subharmonic functions: a) 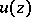 is plurisubharmonic in a domain
is plurisubharmonic in a domain 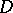 if and only if
if and only if 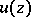 is a plurisubharmonic function in a neighbourhood of each point
is a plurisubharmonic function in a neighbourhood of each point 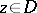 ; b) a linear combination of plurisubharmonic functions with positive coefficients is plurisubharmonic; c) the limit of a uniformly-convergent or monotone decreasing sequence of plurisubharmonic functions is plurisubharmonic; d)
; b) a linear combination of plurisubharmonic functions with positive coefficients is plurisubharmonic; c) the limit of a uniformly-convergent or monotone decreasing sequence of plurisubharmonic functions is plurisubharmonic; d) 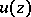 is a plurisubharmonic function in a domain
is a plurisubharmonic function in a domain  if and only if it can be represented as the limit of a decreasing sequence of plurisubharmonic functions
if and only if it can be represented as the limit of a decreasing sequence of plurisubharmonic functions 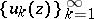 of the classes
of the classes  , respectively, where
, respectively, where 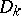 are domains such that
are domains such that 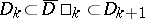 and
and 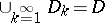 ; e) for any point
; e) for any point 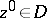 the mean value
the mean value
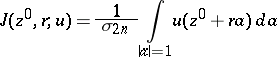 |
over a sphere of radius  , where
, where 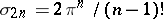 is the area of the unit sphere in
is the area of the unit sphere in 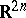 , is an increasing function of
, is an increasing function of  that is convex with respect to
that is convex with respect to 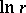 on the segment
on the segment 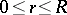 , if the sphere
, if the sphere
 |
is located in 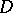 , in which case
, in which case 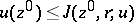 ; f) a plurisubharmonic function remains plurisubharmonic under holomorphic mappings; g) if
; f) a plurisubharmonic function remains plurisubharmonic under holomorphic mappings; g) if 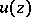 is a continuous plurisubharmonic function in a domain
is a continuous plurisubharmonic function in a domain 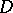 , if
, if 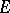 is a closed connected analytic subset of
is a closed connected analytic subset of 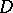 (cf. Analytic set) and if the restriction
(cf. Analytic set) and if the restriction 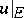 attains a maximum on
attains a maximum on 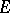 , then
, then 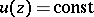 on
on 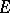 .
.
The following proper subclasses of the class of plurisubharmonic functions are also significant for applications. A function 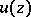 is called strictly plurisubharmonic if there exists a convex increasing function
is called strictly plurisubharmonic if there exists a convex increasing function 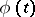 ,
, 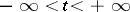 ,
,
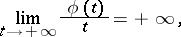 |
such that 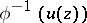 is a plurisubharmonic function. In particular, for
is a plurisubharmonic function. In particular, for 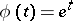 one obtains logarithmically-plurisubharmonic functions.
one obtains logarithmically-plurisubharmonic functions.
The class of plurisubharmonic functions and the above subclasses are important in describing various features of holomorphic functions and domains in the complex space  , as well as in more general analytic spaces [1]–[4], [7]. For example, the class of Hartogs functions
, as well as in more general analytic spaces [1]–[4], [7]. For example, the class of Hartogs functions 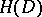 is defined as the smallest class of real-valued functions in
is defined as the smallest class of real-valued functions in 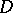 containing all functions
containing all functions 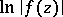 , where
, where 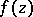 is a holomorphic function in
is a holomorphic function in 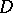 , and closed under the following operations:
, and closed under the following operations:
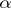 )
) 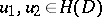 ,
, 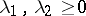 imply
imply 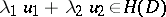 ;
;
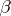 )
) 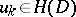 ,
, 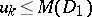 for every domain
for every domain  ,
, 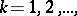 imply
imply 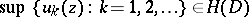 ;
;
 )
) 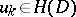 ,
, 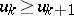 ,
, 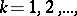 imply
imply 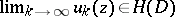 ;
;
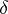 )
) 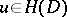 ,
, 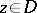 imply
imply 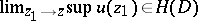 ;
;
 )
) 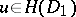 for every subdomain
for every subdomain 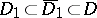 implies
implies 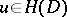 .
.
Upper semi-continuous Hartogs functions are plurisubharmonic, but not every plurisubharmonic function is a Hartogs function. If 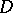 is a domain of holomorphy, the classes of upper semi-continuous Hartogs functions and plurisubharmonic functions in
is a domain of holomorphy, the classes of upper semi-continuous Hartogs functions and plurisubharmonic functions in 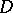 coincide [5], [6].
coincide [5], [6].
See also Pluriharmonic function.
References
| [1] | V.S. Vladimirov, "Methods of the theory of many complex variables" , M.I.T. (1966) (Translated from Russian) |
| [2] | R.C. Gunning, H. Rossi, "Analytic functions of several complex variables" , Prentice-Hall (1965) |
| [3] | P. Lelong, "Fonctions plurisousharmonique; mesures de Radon associées. Applications aux fonctions analytiques" , Colloque sur les fonctions de plusieurs variables, Brussels 1953 , G. Thone & Masson (1953) pp. 21–40 |
| [4] | H.J. Bremermann, "Complex convexity" Trans. Amer. Math. Soc. , 82 (1956) pp. 17–51 |
| [5] | H.J. Bremermann, "On the conjecture of the equivalence of the plurisubharmonic functions and the Hartogs functions" Math. Ann. , 131 (1956) pp. 76–86 |
| [6] | H.J. Bremermann, "Note on plurisubharmonic and Hartogs functions" Proc. Amer. Math. Soc. , 7 (1956) pp. 771–775 |
| [7] | E.D. Solomentsev, "Harmonic and subharmonic functions and their generalizations" Itogi Nauk. Mat. Anal. Teor. Veroyatnost. Regulirovanie (1964) pp. 83–100 (In Russian) |
Comments
A function 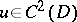 is strictly plurisubharmonic if and only if the complex Hessian
is strictly plurisubharmonic if and only if the complex Hessian 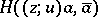 is a positive-definite Hermitian form on
is a positive-definite Hermitian form on  .
.
The Hessian has also an interpretation for arbitrary plurisubharmonic functions  . For every
. For every 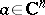 ,
, 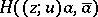 can be viewed as a distribution (cf. Generalized function), which is positive and hence can be represented by a measure. This is in complete analogy with the interpretation of the Laplacian of subharmonic functions.
can be viewed as a distribution (cf. Generalized function), which is positive and hence can be represented by a measure. This is in complete analogy with the interpretation of the Laplacian of subharmonic functions.
However, in this setting one usually introduces currents, cf. [a2]. Let 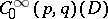 denote the space of compactly-supported differential forms
denote the space of compactly-supported differential forms 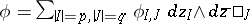 on
on 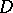 of degree
of degree 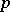 in
in 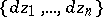 and degree
and degree 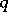 in
in 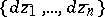 (cf. Differential form). The exterior differential operators
(cf. Differential form). The exterior differential operators 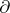 ,
, 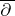 and
and 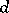 are defined by:
are defined by:
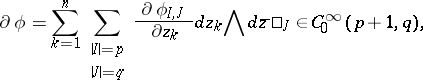 |
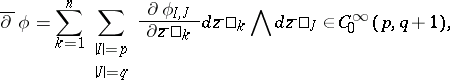 |
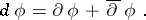 |
The forms in the kernel of 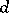 are called closed, the forms in the image of
are called closed, the forms in the image of 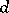 are called exact. As
are called exact. As 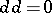 , the set of exact forms is contained in the set of closed forms. A
, the set of exact forms is contained in the set of closed forms. A 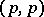 -form is called positive of degree
-form is called positive of degree 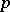 if for every system
if for every system 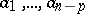 of
of 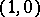 -forms
-forms 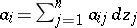 ,
, 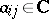 , the
, the 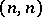 -form
-form  , with
, with 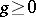 and
and 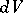 the Euclidean volume element.
the Euclidean volume element.
Let 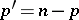 ,
, 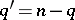 . A
. A  -current
-current 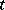 on
on 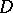 is a linear form
is a linear form 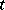 on
on 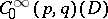 with the property that for every compact set
with the property that for every compact set  there are constants
there are constants 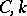 such that
such that 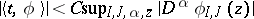 for
for 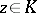 and
and  , where
, where 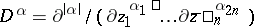 . The operators
. The operators 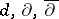 are extended via duality; e.g., if
are extended via duality; e.g., if 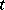 is a
is a 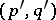 -current, then
-current, then 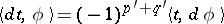 . Closed and exact currents are defined as for differential forms. A
. Closed and exact currents are defined as for differential forms. A 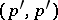 -current is called positive if for every system
-current is called positive if for every system 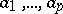 of
of 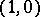 -forms as above and for every
-forms as above and for every  ,
,
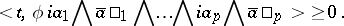 |
A 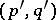 -form
-form 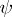 gives rise to a
gives rise to a 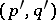 -current
-current 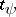 via integration:
via integration: 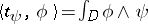 . A complex manifold
. A complex manifold 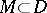 of dimension
of dimension 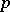 gives rise to a positive closed
gives rise to a positive closed 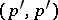 -current
-current 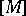 on
on 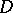 , the current of integration along
, the current of integration along 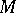 :
:
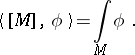 |
The current of integration has also been defined for analytic varieties 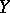 in
in 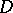 (cf. Analytic manifold): one defines the current of integration for the set of regular points of
(cf. Analytic manifold): one defines the current of integration for the set of regular points of 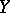 on
on 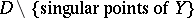 and shows that it can be extended to a positive closed current on
and shows that it can be extended to a positive closed current on 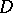 . A plurisubharmonic function
. A plurisubharmonic function 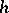 is in
is in 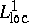 , hence identifies with a
, hence identifies with a 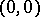 -current. Therefore
-current. Therefore 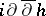 is a
is a 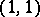 -current, which turns out to be positive and closed. Conversely, a positive closed
-current, which turns out to be positive and closed. Conversely, a positive closed 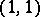 -current is locally of the form
-current is locally of the form 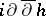 . The current of integration on an irreducible variety of the form
. The current of integration on an irreducible variety of the form 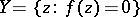 , where
, where 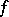 is a holomorphic function with gradient not identically vanishing on
is a holomorphic function with gradient not identically vanishing on 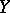 , equals
, equals 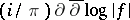 . See also Residue of an analytic function and Residue form.
. See also Residue of an analytic function and Residue form.
References
| [a1] | T.W. Gamelin, "Uniform algebras and Jensen measures" , Cambridge Univ. Press (1979) pp. Chapts. 5; 6 |
| [a2] | P. Lelong, L. Gruman, "Entire functions of several complex variables" , Springer (1980) |
| [a3] | L.I. Ronkin, "Inroduction to the theory of entire functions of several variables" , Transl. Math. Monogr. , 44 , Amer. Math. Soc. (1974) (Translated from Russian) |
| [a4] | R.M. Range, "Holomorphic functions and integral representation in several complex variables" , Springer (1986) pp. Chapt. VI, Par. 6 |
| [a5] | E.M. Chirka, "Complex analytic sets" , Kluwer (1989) pp. 292ff (Translated from Russian) |
Plurisubharmonic function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Plurisubharmonic_function&oldid=13602