Markov chain, ergodic
A homogeneous Markov chain 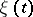 with the following property: There are quantities (independent of
with the following property: There are quantities (independent of 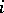 )
)
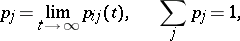 | (1) |
where
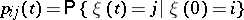 |
are the transition probabilities. The distribution 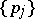 on the state space of the chain
on the state space of the chain 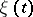 is called a stationary distribution: If
is called a stationary distribution: If 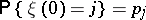 for all
for all 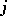 , then
, then 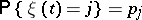 for all
for all 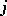 and
and 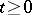 . A fundamental property of Markov chains,
. A fundamental property of Markov chains,
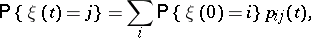 |
enables one to find the 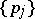 without calculating the limits in (1).
without calculating the limits in (1).
Let
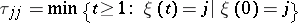 |
be the moment of first return to the state 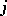 (for a discrete-time Markov chain), then
(for a discrete-time Markov chain), then
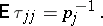 |
A similar (more complicated) relation holds for a continuous-time Markov chain.
The trajectories of an ergodic Markov chain satisfy the ergodic theorem: If 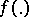 is a function on the state space of the chain
is a function on the state space of the chain 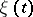 , then, in the discrete-time case,
, then, in the discrete-time case,
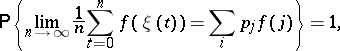 |
while in the continuous-time case the sum on the left is replaced by an integral. A Markov chain for which there are 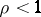 and
and  such that for all
such that for all 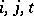 ,
,
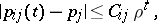 | (2) |
is called geometrically ergodic. A sufficient condition for geometric ergodicity of an ergodic Markov chain is the Doeblin condition (see, for example, [1]), which for a discrete (finite or countable) Markov chain may be stated as follows: There are an 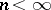 and a state
and a state  such that
such that 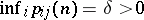 . If the Doeblin condition is satisfied, then for the constants in (2) the relation
. If the Doeblin condition is satisfied, then for the constants in (2) the relation 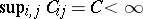 holds.
holds.
A necessary and sufficient condition for geometric ergodicity of a countable discrete-time Markov chain is the following (see [3]): There are numbers 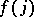 ,
, 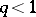 and a finite set
and a finite set 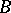 of states such that:
of states such that:
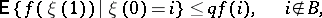 |
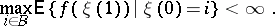 |
References
| [1] | J.L. Doob, "Stochastic processes" , Wiley (1953) |
| [2] | K.L. Chung, "Markov chains with stationary transition probabilities" , Springer (1967) |
| [3] | N.N. Popov, "Conditions for geometric ergodicity of countable Markov chains" Soviet Math. Dokl. , 18 : 3 (1977) pp. 676–679 Dokl. Akad. Nauk SSSR , 234 : 2 (1977) pp. 316–319 |
Comments
References
| [a1] | D. Freedman, "Markov chains" , Holden-Day (1975) |
| [a2] | M. Iosifescu, "Finite Markov processes and their applications" , Wiley (1980) |
| [a3] | J.G. Kemeny, J.L. Snell, "Finite Markov chains" , v. Nostrand (1960) |
| [a4] | J.G. Kemeny, J.L. Snell, A.W. Knapp, "Denumerable Markov chains" , Springer (1976) |
| [a5] | D. Revuz, "Markov chains" , North-Holland (1975) |
| [a6] | V.I. [V.I. Romanovskii] Romanovsky, "Discrete Markov chains" , Wolters-Noordhoff (1970) (Translated from Russian) |
| [a7] | E. Seneta, "Non-negative matrices and Markov chains" , Springer (1981) |
Markov chain, ergodic. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Markov_chain,_ergodic&oldid=13601