Imprimitive group
A group 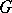 of one-to-one mappings (permutations, cf. Permutation) of a set
of one-to-one mappings (permutations, cf. Permutation) of a set 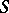 onto itself, for which there exists a partition of
onto itself, for which there exists a partition of 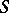 into a union of disjoint subsets
into a union of disjoint subsets 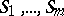 ,
, 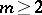 , with the following properties: the number of elements in at least one of the sets
, with the following properties: the number of elements in at least one of the sets 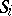 is greater than
is greater than  ; for any permutation
; for any permutation 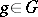 and any
and any 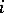 ,
,  , there exists a
, there exists a 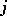 ,
, 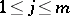 , such that
, such that 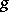 maps
maps 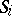 onto
onto 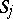 .
.
The collection of subsets 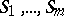 is called a system of imprimitivity, while the subsets
is called a system of imprimitivity, while the subsets 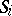 themselves are called domains of imprimitivity of the group
themselves are called domains of imprimitivity of the group 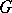 . A non-imprimitive group of permutations is called primitive.
. A non-imprimitive group of permutations is called primitive.
An example of an imprimitive group is a non-trivial intransitive group 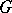 of permutations of a set
of permutations of a set 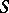 (see Transitive group): for a system of imprimitivity one can take the collection of all orbits (domains of transitivity, cf. Orbit) of
(see Transitive group): for a system of imprimitivity one can take the collection of all orbits (domains of transitivity, cf. Orbit) of 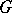 on
on 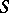 . A transitive group of permutations
. A transitive group of permutations 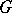 of a set
of a set 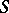 is primitive if and only if for some element (and hence for all elements)
is primitive if and only if for some element (and hence for all elements) 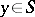 the set of permutations of
the set of permutations of 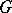 leaving
leaving 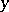 fixed is a maximal subgroup of
fixed is a maximal subgroup of 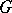 .
.
The notion of an imprimitive group of permutations has an analogue for groups of linear transformations of vector spaces. Namely, a linear representation 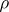 of a group
of a group 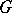 is called imprimitive if there exists a decomposition of the space
is called imprimitive if there exists a decomposition of the space 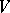 of the representation
of the representation 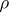 into a direct sum of proper subspaces
into a direct sum of proper subspaces 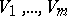 with the following property: For any
with the following property: For any 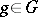 and any
and any 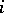 ,
, 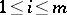 , there exists a
, there exists a 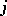 ,
, 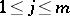 , such that
, such that
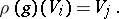 |
The collection of subsets 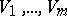 is called a system of imprimitivity of the representation
is called a system of imprimitivity of the representation 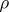 . If
. If 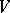 does not have a decomposition of the above type, then
does not have a decomposition of the above type, then 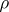 is said to be a primitive representation. An imprimitive representation
is said to be a primitive representation. An imprimitive representation 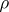 is called transitive imprimitive if there exists for any pair of subspaces
is called transitive imprimitive if there exists for any pair of subspaces 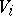 and
and 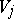 of the system of imprimitivity an element
of the system of imprimitivity an element 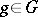 such that
such that 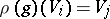 . The group
. The group 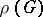 of linear transformations of the space
of linear transformations of the space 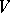 and the
and the 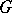 -module
-module 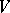 defined by the representation
defined by the representation 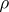 are also called imprimitive (or primitive) if the representation
are also called imprimitive (or primitive) if the representation 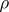 is imprimitive (or primitive).
is imprimitive (or primitive).
Examples. A representation 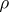 of the symmetric group
of the symmetric group 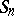 in the
in the  -dimensional vector space over a field
-dimensional vector space over a field 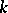 that rearranges the elements of a basis
that rearranges the elements of a basis  is transitive imprimitive, the one-dimensional subspaces
is transitive imprimitive, the one-dimensional subspaces 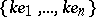 form a system of imprimitivity for
form a system of imprimitivity for 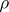 . Another example of a transitive imprimitive representation is the regular representation of a finite group
. Another example of a transitive imprimitive representation is the regular representation of a finite group 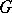 over a field
over a field 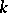 ; the collection of one-dimensional subspaces
; the collection of one-dimensional subspaces 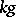 , where
, where 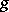 runs through
runs through 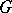 , forms a system of imprimitivity. More generally, any monomial representation of a finite group is imprimitive. The representation of a cyclic group of order
, forms a system of imprimitivity. More generally, any monomial representation of a finite group is imprimitive. The representation of a cyclic group of order 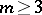 by rotations of the real plane through angles that are multiples of
by rotations of the real plane through angles that are multiples of 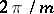 is primitive.
is primitive.
The notion of an imprimitive representation is closely related to that of an induced representation. Namely, let 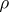 be an imprimitive finite-dimensional representation of a finite group
be an imprimitive finite-dimensional representation of a finite group 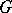 with system of imprimitivity
with system of imprimitivity 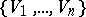 . The set
. The set 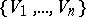 is partitioned into a union of orbits with respect to the action of
is partitioned into a union of orbits with respect to the action of 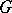 determined by
determined by 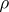 . Let
. Let 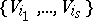 be a complete set of representatives of the different orbits of this action, let
be a complete set of representatives of the different orbits of this action, let
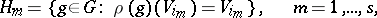 |
let 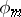 be the representation of the group
be the representation of the group 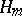 in
in 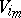 defined by the restriction of
defined by the restriction of 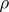 to
to 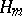 , and let
, and let 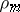 be the representation of
be the representation of 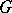 induced by
induced by 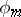 . Then
. Then 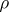 is equivalent to the direct sum of the representations
is equivalent to the direct sum of the representations 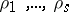 . Conversely, let
. Conversely, let 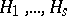 be any collection of subgroups of
be any collection of subgroups of 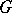 , let
, let 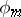 be a representation of
be a representation of 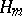 in a finite-dimensional vector space
in a finite-dimensional vector space 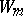 ,
, 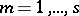 , and let
, and let 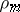 be the representation of
be the representation of 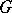 induced by
induced by 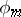 . Suppose further that
. Suppose further that 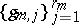 is a system of representatives of left cosets of
is a system of representatives of left cosets of 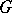 with respect to
with respect to 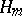 . Then the direct sum of the representations
. Then the direct sum of the representations 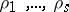 is imprimitive, while
is imprimitive, while 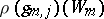 ,
, 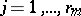 ,
, 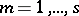 , is a system of imprimitivity (here
, is a system of imprimitivity (here 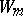 is canonically identified with a subspace of
is canonically identified with a subspace of 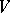 ).
).
References
| [1] | M. Hall, "Group theory" , Macmillan (1959) |
| [2] | C.W. Curtis, I. Reiner, "Representation theory of finite groups and associative algebras" , Interscience (1962) |
Comments
A domain of imprimitivity is also called a block.
Imprimitive group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Imprimitive_group&oldid=13570