Measurable mapping

A mapping 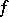of a measurable space 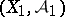to a measurable space 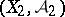such that

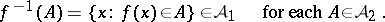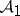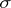In the case where is a -algebra and 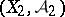is the real line with the 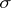-algebra 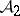of Borel sets (cf. Borel set), the concept of a measurable mapping reduces to that of a measurable function (however, when 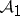is only a 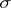-ring, the definition of a measurable function is usually modified in accordance with the requirements of integration theory). The superposition of measurable mappings is measurable. If 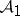and 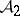are rings and 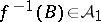for each 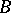in some class of sets 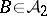such that the ring generated by it is the whole of 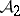, then 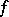is measurable. The analogous assertions hold in the case of 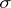-rings, algebras and 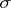-algebras. If 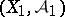and 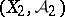are topological spaces with the 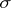-algebras of Borel sets, then every continuous mapping from 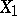to 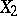is measurable. Let 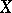be a topological space, let 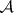be the 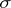-algebra of Borel sets and let 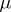be a finite non-negative regular measure on 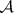(regularity means that 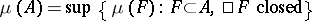). Suppose further that 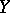is a separable metric space, 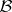is the 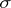-algebra of Borel sets, and let 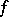be a measurable mapping from 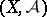to 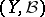. Then for any 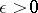there is a closed subset 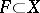such that 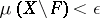and 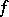is continuous on 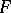(Luzin's theorem).

References

[1]	P.R. Halmos, "Measure theory" , v. Nostrand (1950)
[2]	J. Neveu, "Mathematical foundations of the calculus of probabilities" , Holden-Day (1965) (Translated from French)
[3]	N. Bourbaki, "Elements of mathematics. Integration" , Addison-Wesley (1975) pp. Chapt.6;7;8 (Translated from French)
[4]	N. Dunford, J.T. Schwartz, "Linear operators. General theory" , 1 , Interscience (1958)