Equi-distant
of a set 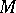 in a metric space
in a metric space 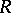
The boundary of the tubular neighbourhood of 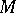 in
in 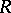 consisting of the balls of the same radius
consisting of the balls of the same radius 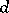 with centres in
with centres in 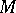 . If
. If 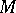 is a differentiable submanifold
is a differentiable submanifold 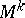 in a Riemannian space
in a Riemannian space 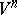 , then the equi-distant of
, then the equi-distant of 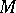 is given (in a more restricted sense) by the set of end-points of the segments of equal length measured from
is given (in a more restricted sense) by the set of end-points of the segments of equal length measured from 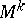 on the geodesics perpendicular to
on the geodesics perpendicular to 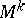 at the corresponding points. If
at the corresponding points. If 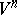 is complete, then the equi-distant is the image under the exponential mapping of the vectors of constant length
is complete, then the equi-distant is the image under the exponential mapping of the vectors of constant length 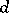 in the normal bundle of
in the normal bundle of 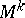 in
in 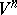 . If
. If 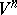 is not complete, then the equi-distant exists only for sufficiently small values of
is not complete, then the equi-distant exists only for sufficiently small values of 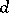 .
.
Examples of equi-distants. 1) An equi-distant in the Lobachevskii plane (a hypercycle) is the orthogonal trajectory of the pencil of straight lines perpendicular to some straight line (to a basic line, or basis). The equi-distant consists of two branches situated on different sides from the basis line and concave towards the basis. The curvature of the equi-distant is constant. 2) An equi-distant in the Lobachevskii space is a surface of constant positive exterior curvature.
Equi-distant. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Equi-distant&oldid=13552