Subdivision
of a geometric simplicial complex 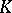
A geometric simplicial complex 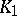 such that the underlying space
such that the underlying space  coincides with the underlying space
coincides with the underlying space  and such that each simplex of
and such that each simplex of 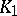 is contained in some simplex of
is contained in some simplex of 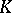 . In practice, the transition to a subdivision is carried out by decomposing the simplices in
. In practice, the transition to a subdivision is carried out by decomposing the simplices in 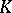 into smaller simplices such that the decomposition of each simplex is matched to the decomposition of its faces. In particular, each vertex of
into smaller simplices such that the decomposition of each simplex is matched to the decomposition of its faces. In particular, each vertex of 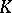 is a vertex of
is a vertex of  . The transition to a subdivision is usually employed to demonstrate invariance of the combinatorially defined characteristics of polyhedra (cf. Polyhedron, abstract; for example, the Euler characteristic or the homology groups, cf. Homology group), and also to obtain triangulations (cf. Triangulation) with the necessary properties (for example, sufficiently small triangulations). A stellar subdivision of a complex
. The transition to a subdivision is usually employed to demonstrate invariance of the combinatorially defined characteristics of polyhedra (cf. Polyhedron, abstract; for example, the Euler characteristic or the homology groups, cf. Homology group), and also to obtain triangulations (cf. Triangulation) with the necessary properties (for example, sufficiently small triangulations). A stellar subdivision of a complex 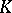 with centre at a point
with centre at a point  is obtained as follows. The closed simplices of
is obtained as follows. The closed simplices of 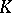 that do not contain
that do not contain  remain unaltered. Each closed simplex
remain unaltered. Each closed simplex 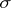 containing
containing  is split up into cones with their vertices at
is split up into cones with their vertices at  over those faces of
over those faces of 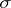 that do not contain
that do not contain  . For any two triangulations
. For any two triangulations 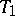 and
and 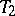 of the same polyhedron
of the same polyhedron 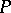 there exists a triangulation
there exists a triangulation 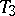 of
of 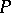 obtained not only from
obtained not only from 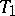 but also from
but also from 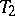 by means of a sequence of stellar subdivisions. The concept of a stellar subdivision may be formalized in the language of abstract simplicial complexes (simplicial schemes). Any stellar subdivision of a closed subcomplex can be extended to a stellar subdivision of the entire complex. The derived complex
by means of a sequence of stellar subdivisions. The concept of a stellar subdivision may be formalized in the language of abstract simplicial complexes (simplicial schemes). Any stellar subdivision of a closed subcomplex can be extended to a stellar subdivision of the entire complex. The derived complex 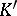 of a complex
of a complex 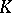 is obtained as the result of a sequence of stellar subdivisions with centres in all open simplices of
is obtained as the result of a sequence of stellar subdivisions with centres in all open simplices of 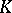 in the order of decreasing dimensions. For an arbitrary closed subcomplex
in the order of decreasing dimensions. For an arbitrary closed subcomplex 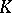 of a complex
of a complex 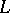 , the subcomplex
, the subcomplex 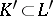 is complete in the following sense: From the fact that all the vertices of a certain simplex
is complete in the following sense: From the fact that all the vertices of a certain simplex 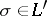 lie in
lie in 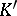 it follows that
it follows that 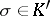 . If one takes as the centres of the derived complex the barycentres of the simplices, one gets the barycentric subdivision. If the diameter of each simplex of an
. If one takes as the centres of the derived complex the barycentres of the simplices, one gets the barycentric subdivision. If the diameter of each simplex of an  -dimensional complex
-dimensional complex 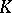 does not exceed
does not exceed 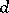 , the diameters of the simplices in its barycentric subdivision are bounded by
, the diameters of the simplices in its barycentric subdivision are bounded by 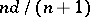 . The diameters of the simplices in the
. The diameters of the simplices in the 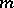 -fold barycentric subdivision of
-fold barycentric subdivision of 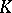 are bounded by
are bounded by 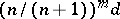 , and so they can be made arbitrarily small by selecting
, and so they can be made arbitrarily small by selecting  sufficiently large.
sufficiently large.
References
| [1] | P.S. Aleksandrov, "Combinatorial topology" , Graylock , Rochester (1956) (Translated from Russian) |
| [2] | P.J. Hilton, S. Wylie, "Homology theory. An introduction to algebraic topology" , Cambridge Univ. Press (1965) |
Comments
References
| [a1] | C.R.F. Maunder, "Algebraic topology" , Cambridge Univ. Press (1980) |
| [a2] | E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966) pp. Sects. 4.4; 5.4 |
Subdivision. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Subdivision&oldid=13515