Nicomedes conchoid
From Encyclopedia of Mathematics
A plane algebraic curve of order 4 whose equation in Cartesian rectangular coordinates has the form
 |
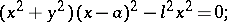and in polar coordinates
 |
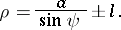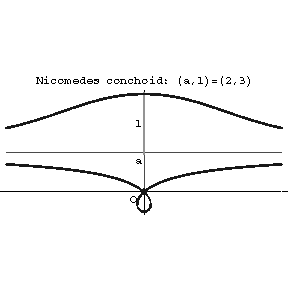
Figure: n066620a
Outer branch (see Fig.). Asymptote 
. Two points of inflection, 
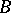and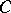 
.
Inner branch. Asymptote 
. The coordinate origin is a double point whose character depends on the values of 
and 
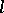. For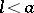 
it is an isolated point and, in addition, the curve has two points of inflection, 
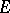and 
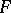; for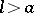 
it is a node; for 
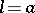it is a cusp. The curve is a conchoid of the straight line 
.
The curve is named after Nicomedes (3rd century B.C.), who used it to solve the problem of trisecting an angle.
References
| [1] | A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian) |
Comments
References
| [a1] | J.D. Lawrence, "A catalog of special plane curves" , Dover, reprint (1972) |
How to Cite This Entry:
Nicomedes conchoid. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Nicomedes_conchoid&oldid=13493
Nicomedes conchoid. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Nicomedes_conchoid&oldid=13493
This article was adapted from an original article by D.D. Sokolov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article