Riemann–Volterra method
A method for solving the Goursat problem and the Cauchy problem for linear hyperbolic partial differential equations of the second order in two independent variables (cf. Hyperbolic partial differential equation),
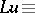 | (1) |
In Riemann's method a fundamental role is played by the Riemann function  which, under suitable conditions on the coefficients
which, under suitable conditions on the coefficients  ,
,  ,
,  , and
, and 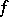 , is defined as the solution of the particular Goursat problem
, is defined as the solution of the particular Goursat problem
with the characteristic boundary conditions
With respect to the variables  , the function
, the function 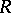 is a solution of the homogeneous equation
is a solution of the homogeneous equation
When 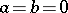 ,
, 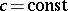 , one has
, one has 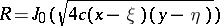 , where
, where  is the Bessel function of order zero.
is the Bessel function of order zero.
The Riemann function may also be defined as the solution of the weighted integral Volterra equation:
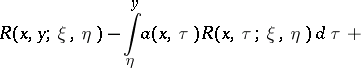 | (2) |
The Riemann method for solving the Goursat problem is as follows: For any function 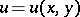 that can be differentiated to the corresponding order, the following identity is valid:
that can be differentiated to the corresponding order, the following identity is valid:
Integrating over the rectangle 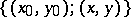 and integrating by parts yields that any solution
and integrating by parts yields that any solution  of (1) is a solution of the weighted integral equation:
of (1) is a solution of the weighted integral equation:
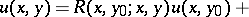 | (3) |
Equation (3) demonstrates directly the well-posedness of the Goursat problem
for equation (1).
Riemann's method solves the Cauchy problem for equation (1) with initial data on any smooth non-characteristic curve by finding a Riemann function. It thus affords the possibility of writing the solution of this problem in the form of quadratures.
Riemann's method has been generalized to a broad class of linear hyperbolic partial differential equations and systems.
In the case of a linear hyperbolic system of partial differential equations of the second order,
where  ,
,  and
and  are given square, real, symmetric matrices of order
are given square, real, symmetric matrices of order  ,
, 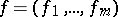 is a given, and
is a given, and 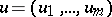 is the unknown vector, the Riemann matrix is unambiguously defined as the solution of a system of weighted Volterra integral equations of the form (2) whose right-hand side is the identity matrix
is the unknown vector, the Riemann matrix is unambiguously defined as the solution of a system of weighted Volterra integral equations of the form (2) whose right-hand side is the identity matrix  of order
of order 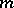 .
.
V. Volterra was the first to generalize Riemann's method to the wave equation
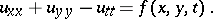 | (4) |
The function
where  , acts as the Riemann function, which permits that the solution of the Cauchy problem with initial data on the plane
, acts as the Riemann function, which permits that the solution of the Cauchy problem with initial data on the plane 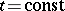 and of the Goursat problem with data on a characteristic cone for equation (4) may be written in the form of quadratures.
and of the Goursat problem with data on a characteristic cone for equation (4) may be written in the form of quadratures.
The method was proposed by B. Riemann (1860).
References
| [1] | A.V. Bitsadse, "Equations of mixed type" , Pergamon (1964) (Translated from Russian) |
| [2] | R. Courant, D. Hilbert, "Methods of mathematical physics. Partial differential equations" , 2 , Interscience (1965) (Translated from German) |
| [3] | V.I. Smirnov, "A course of higher mathematics" , 2 , Addison-Wesley (1964) (Translated from Russian) |
References
| [a1] | P.R. Garabedian, "Partial differential equations" , Wiley (1963) |
How to Cite This Entry:
Riemann method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Riemann_method&oldid=13433
This article was adapted from an original article by A.M. Nakhushev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article
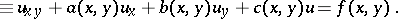
 which, under suitable conditions on the coefficients
which, under suitable conditions on the coefficients  ,
,  ,
,  , and
, and 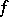 , is defined as the solution of the particular Goursat problem
, is defined as the solution of the particular Goursat problem
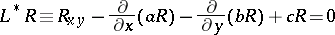
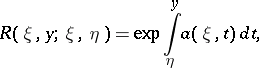
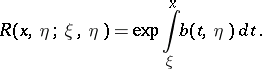
 , the function
, the function 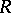 is a solution of the homogeneous equation
is a solution of the homogeneous equation
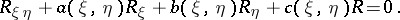
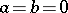 ,
, 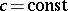 , one has
, one has 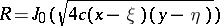 , where
, where  is the Bessel function of order zero.
is the Bessel function of order zero.
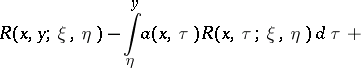
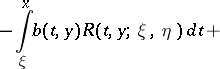

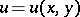 that can be differentiated to the corresponding order, the following identity is valid:
that can be differentiated to the corresponding order, the following identity is valid:

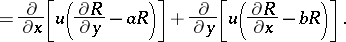
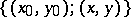 and integrating by parts yields that any solution
and integrating by parts yields that any solution  of (1) is a solution of the weighted integral equation:
of (1) is a solution of the weighted integral equation:
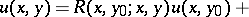
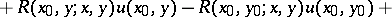

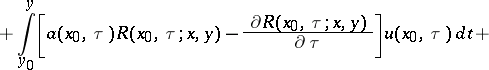
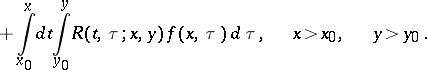
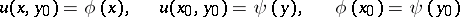
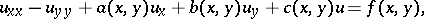
 ,
,  and
and  are given square, real, symmetric matrices of order
are given square, real, symmetric matrices of order  ,
, 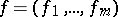 is a given, and
is a given, and 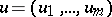 is the unknown vector, the Riemann matrix is unambiguously defined as the solution of a system of weighted Volterra integral equations of the form (2) whose right-hand side is the identity matrix
is the unknown vector, the Riemann matrix is unambiguously defined as the solution of a system of weighted Volterra integral equations of the form (2) whose right-hand side is the identity matrix  of order
of order 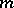 .
.
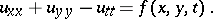

 , acts as the Riemann function, which permits that the solution of the Cauchy problem with initial data on the plane
, acts as the Riemann function, which permits that the solution of the Cauchy problem with initial data on the plane 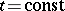 and of the Goursat problem with data on a characteristic cone for equation (4) may be written in the form of quadratures.
and of the Goursat problem with data on a characteristic cone for equation (4) may be written in the form of quadratures.