Algebraic torus
An algebraic group that is isomorphic over some extension of the ground field to the direct product of a finite number of multiplicative groups 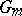 . The group
. The group 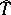 of all algebraic homomorphisms of an algebraic torus
of all algebraic homomorphisms of an algebraic torus 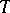 in
in  is known as the character group of
is known as the character group of 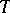 ; it is a free Abelian group of a rank equal to the dimension of
; it is a free Abelian group of a rank equal to the dimension of 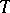 . If the algebraic torus
. If the algebraic torus 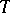 is defined over a field
is defined over a field 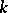 , then
, then 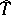 has a
has a 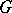 -module structure, where
-module structure, where 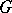 is the Galois group of the separable closure of
is the Galois group of the separable closure of 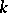 . The functor
. The functor 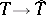 defines a duality between the category of algebraic tori over
defines a duality between the category of algebraic tori over 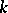 and the category of
and the category of 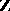 -free
-free 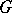 -modules of finite rank. An algebraic torus over
-modules of finite rank. An algebraic torus over 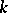 that is isomorphic to a product of groups
that is isomorphic to a product of groups 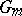 over its ground field
over its ground field 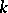 is called split over
is called split over 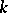 ; any algebraic torus over
; any algebraic torus over  splits over a finite separable extension of
splits over a finite separable extension of 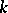 . The role played by algebraic tori in the theory of algebraic groups greatly resembles the role played by tori in the theory of Lie groups. The study of algebraic tori defined over algebraic number fields and other fields, such as finite fields, occupies an important place in problems of arithmetic and in the classification of algebraic groups. Cf. Linear algebraic group; Tamagawa number.
. The role played by algebraic tori in the theory of algebraic groups greatly resembles the role played by tori in the theory of Lie groups. The study of algebraic tori defined over algebraic number fields and other fields, such as finite fields, occupies an important place in problems of arithmetic and in the classification of algebraic groups. Cf. Linear algebraic group; Tamagawa number.
References
| [1] | A. Borel, "Linear algebraic groups" , Benjamin (1969) |
| [2] | T. Ono, "Arithmetic of algebraic tori" Ann. of Math. (2) , 74 : 1 (1961) pp. 101–139 |
| [3] | T. Ono, "On the Tamagawa number of algebraic tori" Ann. of Math. (2) , 78 : 1 (1963) pp. 47–73 |
Algebraic torus. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Algebraic_torus&oldid=13418