Contragredient representation

to a representation 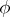of a group 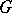in a linear space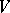

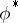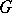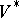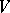The representation of the same group in the dual space of defined by the rule

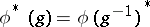for all 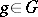, where denotes taking adjoints.

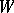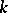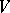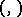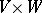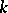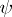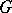More generally, if is a linear space over the same field as and is a non-degenerate bilinear form (pairing) on with values in , then a representation of in 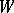is called the representation contragredient to 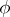with respect to the form 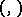if

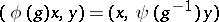for all , , .

For example, if 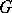is the general linear group of a finite-dimensional space 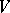, then the natural representation of 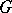in the space of covariant tensors of fixed rank on 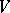is the representation contragredient to the natural representation of 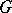in the space of contravariant tensors of the same rank on .

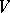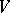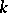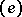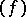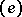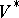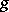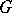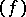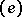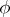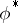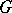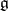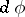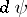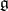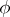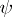Let be finite-dimensional over , let be a basis of it, and let be the basis dual to in . Then, for any in , the matrix of in the basis is obtained from the matrix of the operator in the basis by taking the transpose of the inverse. If is irreducible, then so is . If is a Lie group with Lie algebra , and and are the representations of the algebra induced, respectively, by two representations and of 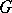in spaces 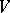and 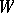that are contragredient with respect to the pairing 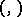, then

(*)

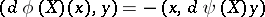for all 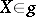, , 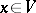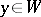. Representations of a Lie algebra 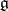satisfying the condition (*) are also called contragredient representations with respect to .

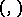Suppose further that 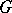is a complex, connected, simply-connected semi-simple Lie group and that 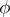is an irreducible finite-dimensional representation of it in a linear space 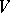. The weights of the representation 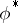are opposite to those of 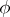(see Weight of a representation of a Lie algebra), the lowest weight of 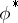being opposite to the highest weight of 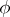(see Cartan theorem on the highest (weight) vector). The representations 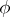and 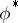are equivalent if and only if there is a non-zero bilinear form on 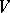that is invariant with respect to 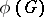. If such a form exists, then it is non-degenerate and either symmetric or skew-symmetric. 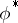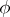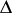The set of numerical marks of the highest weight of the representation is obtained from the set of numerical marks of by applying the substitution induced by the following automorphism of the Dynkin diagram of simple roots of :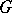

a) takes each connected component 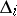, , of 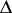into itself;

b) if 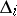is a diagram of type 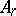, 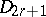or 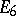, then the restriction of to 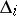is uniquely defined as the unique element of order 2 in the automorphism group of 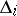; in the remaining cases the restriction of to 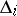is the identity.

References

[1]	M.A. Naimark, "Theory of group representations" , Springer (1982) (Translated from Russian)
[2]	A.A. Kirillov, "Elements of the theory of representations" , Springer (1976) (Translated from Russian)
[3]	D.P. Zhelobenko, "Compact Lie groups and their representations" , Amer. Math. Soc. (1973) (Translated from Russian)
[4]	E.B. Vinberg, A.L. Onishchik, "Seminar on algebraic groups and Lie groups 1967/68" , Springer (Forthcoming) (Translated from Russian)

Comments

If 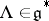is the highest weight of the highest weight representation 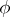, then the set of numerical marks of 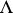is simply the ordered set of integers 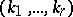, 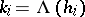; cf. Cartan theorem, especially when written as labels at the corresponding nodes of the Dynkin diagram.