Mapping torus
of an automorphism of a manifold
The mapping torus of a self-mapping 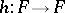 is the identification space
is the identification space
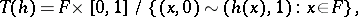 |
which is equipped with a canonical mapping
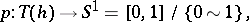 |
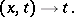 |
If 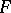 is a closed
is a closed  -dimensional manifold and
-dimensional manifold and 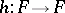 is an automorphism, then
is an automorphism, then 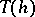 is a closed
is a closed 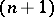 -dimensional manifold such that
-dimensional manifold such that 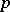 is the projection of a fibre bundle (cf. also Fibration) with fibre
is the projection of a fibre bundle (cf. also Fibration) with fibre  and monodromy
and monodromy 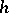 . If
. If 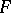 is an
is an  -dimensional manifold with boundary and
-dimensional manifold with boundary and 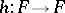 is an automorphism such that
is an automorphism such that 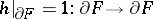 , then
, then 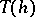 is an
is an 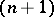 -dimensional manifold with boundary
-dimensional manifold with boundary 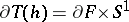 , and the union
, and the union
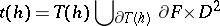 |
is a closed 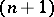 -dimensional manifold, called an open book. It is important to know when manifolds are fibre bundles over
-dimensional manifold, called an open book. It is important to know when manifolds are fibre bundles over 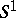 and open books, for in those cases the classification of
and open books, for in those cases the classification of 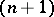 -dimensional manifolds is reduced to the classification of automorphisms of
-dimensional manifolds is reduced to the classification of automorphisms of  -dimensional manifolds.
-dimensional manifolds.
A codimension- submanifold
submanifold  is fibred if it has a neighbourhood
is fibred if it has a neighbourhood 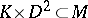 such that the exterior
such that the exterior 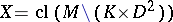 is a mapping torus, i.e. if
is a mapping torus, i.e. if 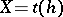 is an open book for some automorphism
is an open book for some automorphism 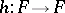 of a codimension-
of a codimension-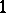 submanifold
submanifold 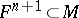 with
with 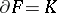 (a Seifert surface, cf. Seifert manifold). Fibred knots
(a Seifert surface, cf. Seifert manifold). Fibred knots 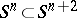 and fibred links
and fibred links 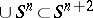 have particularly strong geometric and algebraic properties (cf. also Knot and link diagrams; Knot theory).
have particularly strong geometric and algebraic properties (cf. also Knot and link diagrams; Knot theory).
In 1923, J.W. Alexander used geometry to prove that every closed  -dimensional manifold
-dimensional manifold  is an open book, that is, there exists a fibred link
is an open book, that is, there exists a fibred link 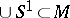 , generalizing the Heegaard splitting.
, generalizing the Heegaard splitting.
Fibred knots 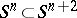 came to prominence in the 1960s with the influential work of J. Milnor on singular points of complex hypersurfaces, and with the examples of E. Brieskorn realizing the exotic spheres as links of singular points.
came to prominence in the 1960s with the influential work of J. Milnor on singular points of complex hypersurfaces, and with the examples of E. Brieskorn realizing the exotic spheres as links of singular points.
Connected infinite cyclic coverings  of a connected space
of a connected space 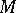 are in one-one correspondence with expressions of the fundamental group
are in one-one correspondence with expressions of the fundamental group 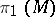 as a group extension
as a group extension
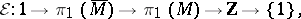 |
and also with the homotopy classes of mappings 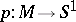 inducing surjections
inducing surjections 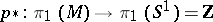 . If
. If 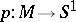 is the projection of a fibre bundle with
is the projection of a fibre bundle with 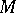 compact, the non-compact space
compact, the non-compact space 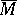 is homotopy equivalent (cf. also Homotopy type) to the fibre
is homotopy equivalent (cf. also Homotopy type) to the fibre 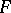 , which is compact, so that the fundamental group
, which is compact, so that the fundamental group 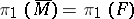 and the homology groups
and the homology groups 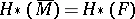 are finitely generated.
are finitely generated.
In 1962, J. Stallings used group theory to prove that if 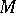 is an irreducible closed
is an irreducible closed  -dimensional manifold with
-dimensional manifold with 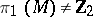 and with an extension
and with an extension 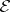 such that
such that 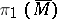 is finitely generated (cf. also Finitely-generated group), then
is finitely generated (cf. also Finitely-generated group), then  is a fibre bundle over
is a fibre bundle over 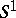 , with
, with 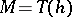 for some automorphism
for some automorphism 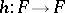 of a surface
of a surface 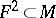 . In 1964, W. Browder and J. Levine used simply-connected surgery to prove that for
. In 1964, W. Browder and J. Levine used simply-connected surgery to prove that for 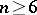 every closed
every closed  -dimensional manifold
-dimensional manifold 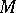 with
with 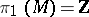 and
and 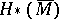 finitely generated, is a fibre bundle over
finitely generated, is a fibre bundle over 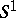 . In 1984, M. Kreck used this type of surgery to compute the bordism groups
. In 1984, M. Kreck used this type of surgery to compute the bordism groups 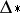 of automorphisms of high-dimensional manifolds and to evaluate the mapping-torus mapping
of automorphisms of high-dimensional manifolds and to evaluate the mapping-torus mapping
 |
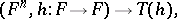 |
to the ordinary bordism over 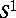 (cf. also Bordism).
(cf. also Bordism).
A band is a compact manifold 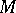 with a connected infinite cyclic covering
with a connected infinite cyclic covering 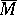 which is finitely dominated, i.e. such that there exists a finite CW-complex
which is finitely dominated, i.e. such that there exists a finite CW-complex 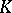 with mappings
with mappings 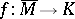 ,
, 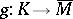 and a homotopy
and a homotopy 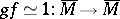 . In 1968, F.T. Farrell used non-simply-connected surgery theory to prove that for
. In 1968, F.T. Farrell used non-simply-connected surgery theory to prove that for  a piecewise-linear (or differentiable)
a piecewise-linear (or differentiable)  -dimensional manifold band
-dimensional manifold band 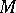 is a fibre bundle over
is a fibre bundle over 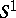 if and only if a Whitehead torsion obstruction
if and only if a Whitehead torsion obstruction 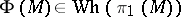 is
is  . The theorem was important in the structure theory of high-dimensional topological manifolds, and in 1970 was extended to topological manifolds by L. Siebenmann. There is also a version for Hilbert cube manifolds, obtained in 1974 by T.A. Chapman and Siebenmann. The fibering obstruction
. The theorem was important in the structure theory of high-dimensional topological manifolds, and in 1970 was extended to topological manifolds by L. Siebenmann. There is also a version for Hilbert cube manifolds, obtained in 1974 by T.A. Chapman and Siebenmann. The fibering obstruction 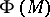 for finite-dimensional
for finite-dimensional 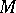 measures the difference between the intrinsic simple homotopy type of
measures the difference between the intrinsic simple homotopy type of 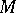 given by a handle-body decomposition and the extrinsic simple homotopy type given by
given by a handle-body decomposition and the extrinsic simple homotopy type given by 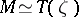 with
with 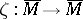 a generating covering translation.
a generating covering translation.
In 1972, H.E. Winkelnkemper used surgery to prove that for 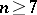 a simply-connected
a simply-connected  -dimensional manifold
-dimensional manifold 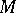 is an open book if and only if the signature of
is an open book if and only if the signature of 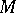 is
is  . In 1977, T. Lawson used non-simply-connected surgery to prove that for odd
. In 1977, T. Lawson used non-simply-connected surgery to prove that for odd 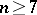 every
every  -dimensional manifold
-dimensional manifold 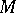 is an open book. In 1979, F. Quinn used non-simply-connected surgery to prove that for even
is an open book. In 1979, F. Quinn used non-simply-connected surgery to prove that for even 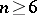 an
an  -dimensional manifold
-dimensional manifold 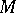 is an open book if and only if an obstruction in the asymmetric Witt group of
is an open book if and only if an obstruction in the asymmetric Witt group of 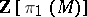 vanishes, generalizing the Wall surgery obstruction (cf. also Witt decomposition).
vanishes, generalizing the Wall surgery obstruction (cf. also Witt decomposition).
For a recent account of fibre bundles over 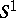 and open books see [a1].
and open books see [a1].
References
| [a1] | A. Ranicki, "High-dimensional knot theory" , Springer (1998) |
Mapping torus. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Mapping_torus&oldid=13400