Extension of a field
field extension
A field containing the given field as a subfield. The notation 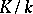 means that
means that 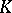 is an extension of the field
is an extension of the field 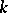 . In this case,
. In this case, 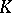 is sometimes called an overfield of the field
is sometimes called an overfield of the field 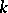 .
.
Let 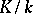 and
and 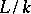 be two extensions of a field
be two extensions of a field 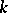 . An isomorphism of fields
. An isomorphism of fields 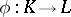 is called an isomorphism of extensions (or a
is called an isomorphism of extensions (or a 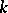 -isomorphism of fields) if
-isomorphism of fields) if  is the identity on
is the identity on 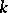 . If an isomorphism of extensions exists, then the extensions are said to be isomorphic. If
. If an isomorphism of extensions exists, then the extensions are said to be isomorphic. If 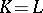 ,
, 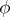 is called an automorphism of the extension
is called an automorphism of the extension 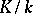 . The set of all automorphisms of an extension forms a group,
. The set of all automorphisms of an extension forms a group, 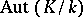 . If
. If 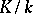 is a Galois extension, this group is denoted by
is a Galois extension, this group is denoted by 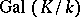 and is called the Galois group of the field
and is called the Galois group of the field 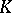 over
over 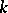 , or the Galois group of the extension
, or the Galois group of the extension 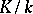 . An extension is called Abelian if its Galois group is Abelian.
. An extension is called Abelian if its Galois group is Abelian.
An element 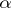 of the field
of the field 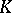 is called algebraic over
is called algebraic over 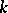 if it satisfies some algebraic equation with coefficients in
if it satisfies some algebraic equation with coefficients in 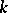 , and transcendental otherwise. For every algebraic element
, and transcendental otherwise. For every algebraic element 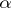 there is a unique polynomial
there is a unique polynomial 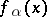 , with leading coefficient equal to 1, that is irreducible in the polynomial ring
, with leading coefficient equal to 1, that is irreducible in the polynomial ring 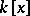 and satisfies
and satisfies 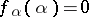 ; any polynomial over
; any polynomial over 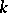 having
having 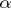 as a root is divisible by
as a root is divisible by 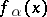 . This polynomial is called the minimal polynomial of
. This polynomial is called the minimal polynomial of 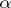 . An extension
. An extension 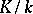 is called algebraic if every element of
is called algebraic if every element of 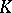 is algebraic over
is algebraic over 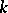 . An extension that is not algebraic is called transcendental. An extension is called normal if it is algebraic and if every irreducible polynomial in
. An extension that is not algebraic is called transcendental. An extension is called normal if it is algebraic and if every irreducible polynomial in 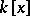 having a root in
having a root in 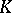 factorizes into linear factors in
factorizes into linear factors in 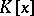 . The subfield
. The subfield 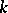 is said to be algebraically closed in
is said to be algebraically closed in 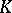 if every element of
if every element of 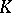 that is algebraic over
that is algebraic over 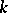 actually lies in
actually lies in 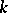 , that is, every element of
, that is, every element of 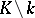 is transcendental over
is transcendental over 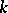 . A field that is algebraically closed in all its extensions is called an algebraically closed field.
. A field that is algebraically closed in all its extensions is called an algebraically closed field.
An extension 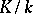 is said to be finitely generated (or an extension of finite type) if there is a finite subset
is said to be finitely generated (or an extension of finite type) if there is a finite subset 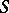 of
of 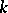 such that
such that 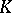 coincides with the smallest subfield containing
coincides with the smallest subfield containing 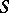 and
and 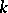 . In this case one says that
. In this case one says that 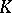 is generated by
is generated by 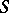 over
over 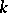 . If
. If 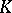 is generated over
is generated over 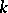 by one element
by one element 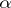 , then the extension is called simple or primitive and one writes
, then the extension is called simple or primitive and one writes 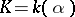 . A simple algebraic extension
. A simple algebraic extension 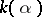 is completely determined by the minimal polynomial
is completely determined by the minimal polynomial 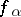 of
of 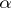 . More precisely, if
. More precisely, if 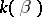 is another simple algebraic extension and
is another simple algebraic extension and 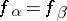 , then there is an isomorphism of extensions
, then there is an isomorphism of extensions 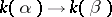 sending
sending 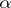 to
to 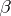 . Furthermore, for any irreducible polynomial
. Furthermore, for any irreducible polynomial 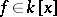 there is a simple algebraic extension
there is a simple algebraic extension 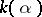 with minimal polynomial
with minimal polynomial 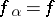 . It can be constructed as the quotient ring
. It can be constructed as the quotient ring 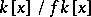 . On the other hand, for any simple transcendental extension
. On the other hand, for any simple transcendental extension 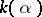 there is an isomorphism of extensions
there is an isomorphism of extensions 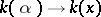 , where
, where 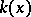 is the field of rational functions in
is the field of rational functions in  over
over 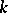 . Any extension of finite type can be obtained by performing a finite sequence of simple extensions.
. Any extension of finite type can be obtained by performing a finite sequence of simple extensions.
An extension 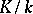 is called finite if
is called finite if 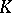 is finite-dimensional as a vector space over
is finite-dimensional as a vector space over 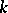 , and infinite otherwise. The dimension of this vector space is called the degree of
, and infinite otherwise. The dimension of this vector space is called the degree of 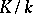 and is denoted by
and is denoted by 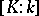 . Every finite extension is algebraic and every algebraic extension of finite type is finite. The degree of a simple algebraic extension coincides with the degree of the corresponding minimal polynomial. On the other hand, a simple transcendental extension is infinite.
. Every finite extension is algebraic and every algebraic extension of finite type is finite. The degree of a simple algebraic extension coincides with the degree of the corresponding minimal polynomial. On the other hand, a simple transcendental extension is infinite.
Suppose one is given a sequence of extensions 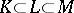 . Then
. Then 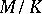 is algebraic if and only if both
is algebraic if and only if both 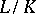 and
and 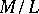 are. Further,
are. Further, 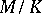 is finite if and only if
is finite if and only if 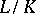 and
and 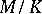 are, and then
are, and then
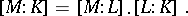 |
If 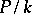 and
and 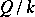 are two algebraic extensions and
are two algebraic extensions and 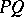 is the compositum of the fields
is the compositum of the fields 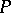 and
and 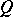 in a common overfield, then
in a common overfield, then 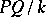 is also algebraic.
is also algebraic.
See also Separable extension; Transcendental extension.
References
| [1] | N. Bourbaki, "Eléments de mathématique. Algèbre" , Masson (1981) pp. Chapt. 4–7 |
| [2] | B.L. van der Waerden, "Algebra" , 1–2 , Springer (1967–1971) (Translated from German) |
| [3] | O. Zariski, P. Samuel, "Commutative algebra" , 1 , Springer (1975) |
| [4] | S. Lang, "Algebra" , Addison-Wesley (1974) |
Extension of a field. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Extension_of_a_field&oldid=13369