Covariance matrix
The matrix formed from the pairwise covariances of several random variables; more precisely, for the  -dimensional vector
-dimensional vector  the covariance matrix is the square matrix
the covariance matrix is the square matrix  , where
, where  is the vector of mean values. The components of the covariance matrix are:
is the vector of mean values. The components of the covariance matrix are:
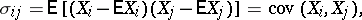 |
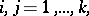 |
and for  they are the same as
they are the same as  (
( ) (that is, the variances of the
) (that is, the variances of the 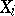 lie on the principal diagonal). The covariance matrix is a symmetric positive semi-definite matrix. If the covariance matrix is positive definite, then the distribution of
lie on the principal diagonal). The covariance matrix is a symmetric positive semi-definite matrix. If the covariance matrix is positive definite, then the distribution of  is non-degenerate; otherwise it is degenerate. For the random vector
is non-degenerate; otherwise it is degenerate. For the random vector 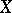 the covariance matrix plays the same role as the variance of a random variable. If the variances of the random variables
the covariance matrix plays the same role as the variance of a random variable. If the variances of the random variables 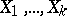 are all equal to 1, then the covariance matrix of
are all equal to 1, then the covariance matrix of  is the same as the correlation matrix.
is the same as the correlation matrix.
The sample covariance matrix for the sample  , where the
, where the  ,
,  , are independent and identically-distributed random
, are independent and identically-distributed random 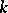 -dimensional vectors, consists of the variance and covariance estimators:
-dimensional vectors, consists of the variance and covariance estimators:
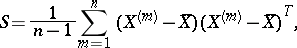 |
where the vector 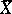 is the arithmetic mean of the
is the arithmetic mean of the  . If the
. If the  are multivariate normally distributed with covariance matrix
are multivariate normally distributed with covariance matrix  , then
, then  is the maximum-likelihood estimator of
is the maximum-likelihood estimator of 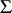 ; in this case the joint distribution of the elements of the matrix
; in this case the joint distribution of the elements of the matrix  is called the Wishart distribution; it is one of the fundamental distributions in multivariate statistical analysis by means of which hypotheses concerning the covariance matrix
is called the Wishart distribution; it is one of the fundamental distributions in multivariate statistical analysis by means of which hypotheses concerning the covariance matrix 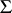 can be tested.
can be tested.
Covariance matrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Covariance_matrix&oldid=13365