Sesquilinear form
A function in two variables on a module (for example, on a vector space) which is linear in one variable and semi-linear in the other. More precisely, a sesquilinear form on a unitary module  over an associative-commutative ring
over an associative-commutative ring  with an identity, equipped with an automorphism
with an identity, equipped with an automorphism  , is a mapping
, is a mapping  ,
,  , linear in
, linear in  for fixed
for fixed  , and semi-linear in
, and semi-linear in  for fixed
for fixed  (see Semi-linear mapping). Analogously one defines a sesquilinear mapping
(see Semi-linear mapping). Analogously one defines a sesquilinear mapping 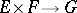 , where
, where  ,
,  ,
, 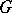 are
are  -modules. In the case when
-modules. In the case when 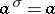 (
( ), one obtains the notion of a bilinear form (or a bilinear mapping). Another important example of a sesquilinear form is obtained when
), one obtains the notion of a bilinear form (or a bilinear mapping). Another important example of a sesquilinear form is obtained when 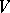 is a vector space over the field
is a vector space over the field  and
and  . Special cases of sesquilinear forms are Hermitian forms (cf. Hermitian form) (and also skew-Hermitian forms).
. Special cases of sesquilinear forms are Hermitian forms (cf. Hermitian form) (and also skew-Hermitian forms).
Sesquilinear forms can also be considered on modules over a non-commutative ring 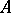 ; in this case it is assumed that
; in this case it is assumed that 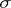 is an anti-automorphism, that is,
is an anti-automorphism, that is,
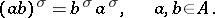 |
For sesquilinear forms it is possible to introduce many notions of the theory of bilinear forms, for example the notions of an orthogonal submodule, a left and a right kernel, a non-degenerate form, the matrix of the form in a given basis, the rank of the form, and conjugate homomorphisms.
References
| [1] | N. Bourbaki, "Algèbre" , Eléments de mathématiques , 2 , Hermann (1942–1959) |
| [2] | S. Lang, "Algebra" , Addison-Wesley (1984) |
Comments
Let 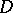 be a division ring with centre
be a division ring with centre  and
and  a right vector space over
a right vector space over 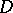 . Let
. Let  be an anti-automorphism of
be an anti-automorphism of  , i.e.
, i.e.  is an automorphism of the underlying additive group of
is an automorphism of the underlying additive group of  and
and  . A sesquilinear form relative to
. A sesquilinear form relative to  on
on  is a bi-additive mapping
is a bi-additive mapping
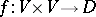 |
such that
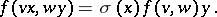 |
Unless  , the anti-automorphism
, the anti-automorphism  is obviously uniquely determined by
is obviously uniquely determined by  .
.
Let  . A
. A 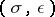 -Hermitian form is a sesquilinear form on
-Hermitian form is a sesquilinear form on  such that moreover
such that moreover
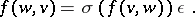 |
One must then have  and
and  for all
for all  . The concepts of a Hermitian, anti-Hermitian, symmetric, anti-symmetric, or bilinear form (or matrix) for complex vector spaces (with
. The concepts of a Hermitian, anti-Hermitian, symmetric, anti-symmetric, or bilinear form (or matrix) for complex vector spaces (with  complex conjugation) arise as the special cases of a
complex conjugation) arise as the special cases of a 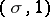 -Hermitian form, a
-Hermitian form, a  -Hermitian form, an
-Hermitian form, an  -Hermitian form, and an
-Hermitian form, and an  Hermitian form.
Hermitian form.
Given a subspace  ,
, 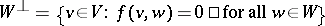 . A subspace
. A subspace 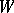 is totally isotropic if
is totally isotropic if  . The Witt index of a sesquilinear form is the dimension of a maximal totally-isotropic subspace.
. The Witt index of a sesquilinear form is the dimension of a maximal totally-isotropic subspace.
References
| [a1] | J. Tits, "Buildings and BN-pairs of spherical type" , Springer (1974) pp. Chapt. 8 |
| [a2] | J.A. Dieudonné, "La géométrie des groups classiques" , Springer (1963) |
Sesquilinear form. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sesquilinear_form&oldid=13338