Stochastic sequence
A sequence of random variables 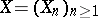 , defined on a measure space
, defined on a measure space 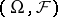 with an increasing family of
with an increasing family of 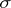 -algebras
-algebras 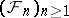 ,
, 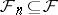 , on it, which is adapted: For every
, on it, which is adapted: For every 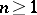 ,
, 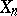 is
is 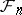 -measurable. In writing such sequences, the notation
-measurable. In writing such sequences, the notation 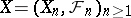 is often used, stressing the measurability of
is often used, stressing the measurability of 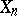 relative to
relative to 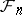 . Typical examples of stochastic sequences defined on a probability space
. Typical examples of stochastic sequences defined on a probability space 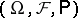 are Markov sequences, martingales, semi-martingales, and others (cf. Markov chain; Martingale; Semi-martingale). In the case of continuous time (where the discrete time
are Markov sequences, martingales, semi-martingales, and others (cf. Markov chain; Martingale; Semi-martingale). In the case of continuous time (where the discrete time 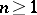 is replaced by
is replaced by 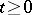 ), the corresponding aggregate of objects
), the corresponding aggregate of objects 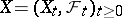 is called a stochastic process.
is called a stochastic process.
Comments
The expression "stochastic sequence" is rarely used in the West; one usually says "stochastic process" and adds "with discrete time" if necessary. Strictly speaking, it is just a sequence of random variables, but often, when a filtration 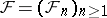 is given, one assumes, as in the main article, adaptation of the process. Cf. also Stochastic process, compatible.
is given, one assumes, as in the main article, adaptation of the process. Cf. also Stochastic process, compatible.
Stochastic sequence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stochastic_sequence&oldid=13334