Pi-separable group
A group which has a normal series such that the order of every factor contains at most one prime from 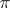 (
(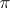 is a set of prime numbers). The class of
is a set of prime numbers). The class of 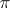 -separable groups contains the class of
-separable groups contains the class of 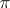 -solvable groups (cf.
-solvable groups (cf. 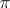 -solvable group). For finite
-solvable group). For finite 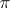 -separable groups, the
-separable groups, the  -Sylow properties (cf. Sylow theorems) have been shown to hold (see [1]). In fact, for any set
-Sylow properties (cf. Sylow theorems) have been shown to hold (see [1]). In fact, for any set 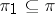 , a finite
, a finite 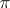 -separable group
-separable group  contains a
contains a 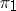 -Hall subgroup (cf. also Hall subgroup), and any two
-Hall subgroup (cf. also Hall subgroup), and any two 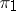 -Hall subgroups are conjugate in
-Hall subgroups are conjugate in 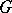 . Any
. Any 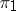 -subgroup of a
-subgroup of a 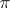 -separable group
-separable group 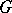 is contained in some
is contained in some 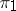 -Hall subgroup of
-Hall subgroup of  (see [2]).
(see [2]).
References
| [1] | S.A. Chunikhin, "On 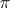 -separable groups" Dokl. Akad. Nauk SSSR , 59 : 3 (1948) pp. 443–445 (In Russian) -separable groups" Dokl. Akad. Nauk SSSR , 59 : 3 (1948) pp. 443–445 (In Russian) |
| [2] | P. Hall, "Theorems like Sylow's" Proc. London Math. Soc. , 6 : 22 (1956) pp. 286–304 |
Comments
Chunikhin's theorem says that if 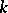 is a divisor of the order
is a divisor of the order  of a
of a 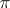 -separable group such that
-separable group such that 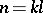 ,
, 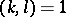 , and if all prime divisors of
, and if all prime divisors of 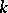 are in
are in  , then
, then 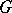 has a subgroup of order
has a subgroup of order  and all these subgroups are conjugate in
and all these subgroups are conjugate in 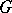 . If
. If 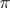 consists of all prime numbers this becomes Hall's first theorem.
consists of all prime numbers this becomes Hall's first theorem.
Gol'berg's theorem, [a2], says that if 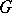 is a finite
is a finite 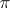 -separable group and
-separable group and 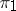 is a subset of
is a subset of  , then
, then 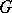 has a Sylow
has a Sylow 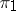 -basis (cf. Sylow basis) and all these bases are conjugate.
-basis (cf. Sylow basis) and all these bases are conjugate.
References
| [a1] | A.G. Kurosh, "The theory of groups" , 2 , Chelsea (1956) pp. 195ff (Translated from Russian) |
| [a2] | P.A. Gol'berg, "Sylow bases of 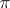 -separable groups" Dokl. Akad. Nauk SSSR , 60 (1949) pp. 615–618 (In Russian) -separable groups" Dokl. Akad. Nauk SSSR , 60 (1949) pp. 615–618 (In Russian) |
| [a3] | S.A. Chunikhin, "On 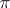 -properties of finite groups" Mat. Sb. , 25 (1949) pp. 321–346 (In Russian) -properties of finite groups" Mat. Sb. , 25 (1949) pp. 321–346 (In Russian) |
Pi-separable group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pi-separable_group&oldid=13312