Open-mapping theorem
A continuous linear operator 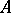 mapping a Banach space
mapping a Banach space 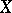 onto all of a Banach space
onto all of a Banach space  is an open mapping, i.e.
is an open mapping, i.e.  is open in
is open in 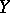 for any
for any 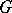 which is open in
which is open in 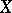 . This was proved by S. Banach. Furthermore, a continuous linear operator
. This was proved by S. Banach. Furthermore, a continuous linear operator 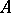 giving a one-to-one transformation of a Banach space
giving a one-to-one transformation of a Banach space 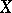 onto a Banach space
onto a Banach space 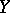 is a homeomorphism, i.e.
is a homeomorphism, i.e. 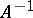 is also a continuous linear operator (Banach's homeomorphism theorem).
is also a continuous linear operator (Banach's homeomorphism theorem).
The conditions of the open-mapping theorem are satisfied, for example, by every non-zero continuous linear functional defined on a real (complex) Banach space 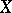 with values in
with values in 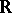 (in
(in 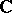 ).
).
The open-mapping theorem can be generalized as follows: A continuous linear operator mapping a fully-complete (or  -complete) topological vector space
-complete) topological vector space  onto a barrelled space
onto a barrelled space 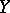 is an open mapping. The closed-graph theorem can be considered alongside with the open-mapping theorem.
is an open mapping. The closed-graph theorem can be considered alongside with the open-mapping theorem.
References
| [1] | K. Yosida, "Functional analysis" , Springer (1980) |
| [2] | A.P. Robertson, W.S. Robertson, "Topological vector spaces" , Cambridge Univ. Press (1964) |
Comments
A recent comprehensive study of the closed-graph theorem can be found in [a1].
References
| [a1] | M. de Wilde, "Closed graph theorems and webbed spaces" , Pitman (1978) |
| [a2] | H.H. Schaefer, "Topological vector spaces" , Springer (1971) |
| [a3] | H. Jarchow, "Locally convex spaces" , Teubner (1981) (Translated from German) |
Open-mapping theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Open-mapping_theorem&oldid=13271