Shapley value
A vector function 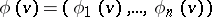 defined on the set of characteristic functions of
defined on the set of characteristic functions of  -person games and satisfying the following axioms: 1) (efficiency) if a coalition
-person games and satisfying the following axioms: 1) (efficiency) if a coalition 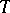 is such that for any coalition
is such that for any coalition 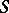 the equality
the equality 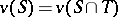 holds, then
holds, then 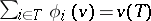 ; 2) (symmetry) if
; 2) (symmetry) if 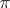 is a permutation of the set
is a permutation of the set 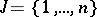 and if for any coalition
and if for any coalition 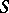 the equality
the equality 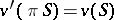 holds, then
holds, then 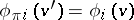 ; and 3) (linearity)
; and 3) (linearity) 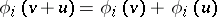 . These axioms were introduced by L.S. Shapley [1] for an axiomatic definition of the expected pay-off in a cooperative game. It has been shown that the only vector function satisfying the axioms 1)–3) is
. These axioms were introduced by L.S. Shapley [1] for an axiomatic definition of the expected pay-off in a cooperative game. It has been shown that the only vector function satisfying the axioms 1)–3) is
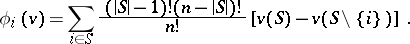 |
References
| [1] | L.S. Shapley, "A value for  -person games" , Contributions to the theory of games , 2 , Princeton Univ. Press (1953) pp. 307–317 -person games" , Contributions to the theory of games , 2 , Princeton Univ. Press (1953) pp. 307–317 |
Comments
The concept of Shapley value has been modified (by several authors) by considering alternative axioms. Many applications to computations of indices of power and to various economic situations have been given. The value has also been defined for games with infinitely many players.
References
| [a1] | R.J. Aumann, L.S. Shapley, "Values of non-atomic games" , Princeton Univ. Press (1974) |
| [a2] | G. Owen, "Game theory" , Acad. Press (1982) |
| [a3] | J.W. Friedman, "Oligopoly and the theory of games" , North-Holland (1977) |
Shapley value. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Shapley_value&oldid=13254