Morera theorem
If a (single-valued) function 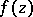 of a complex variable
of a complex variable  in a domain
in a domain 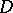 is continuous and if its integral over any closed rectifiable contour
is continuous and if its integral over any closed rectifiable contour 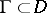 is equal to zero, that is, if
is equal to zero, that is, if
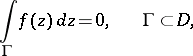 | (*) |
then 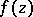 is an analytic function in
is an analytic function in 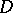 . This theorem was obtained by G. Morera [1].
. This theorem was obtained by G. Morera [1].
The conditions of Morera's theorem can be weakened by restricting the requirement on vanishing integrals (*) to those taken over the boundary 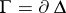 of any triangle
of any triangle 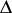 that is compactly contained in
that is compactly contained in 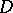 , i.e. such that
, i.e. such that  . Morera's theorem is an (incomplete) converse of the Cauchy integral theorem and is one of the basic theorems in the theory of analytic functions.
. Morera's theorem is an (incomplete) converse of the Cauchy integral theorem and is one of the basic theorems in the theory of analytic functions.
Morera's theorem can be generalized to functions of several complex variables. Let 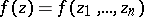 be a function of the complex variables
be a function of the complex variables  ,
, 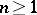 , continuous in a domain
, continuous in a domain 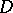 of
of 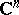 and such that its integral vanishes when taken over the boundary
and such that its integral vanishes when taken over the boundary 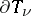 of any prismatic domain compactly contained in
of any prismatic domain compactly contained in 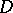 of the form
of the form
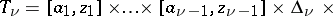 |
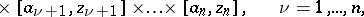 |
where 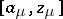 ,
, 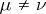 ,
, 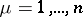 , are line segments in the planes
, are line segments in the planes 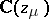 with end points
with end points 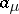 and
and 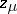 , and
, and 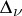 is a triangle in the plane
is a triangle in the plane 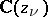 . Then
. Then 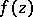 is a holomorphic function in
is a holomorphic function in 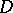 .
.
References
| [1] | G. Morera, "Un teorema fondamentale nella teorica delle funzioni di una variabili complessa" Rend. R. Ist. Lomb. Sci. Lettere , 19 (1886) pp. 304–308 |
| [2] | A.I. Markushevich, "Theory of functions of a complex variable" , 1 , Chelsea (1977) (Translated from Russian) |
| [3] | B.V. Shabat, "Introduction of complex analysis" , 1–2 , Moscow (1976) (In Russian) |
| [4] | V.S. Vladimirov, "Methods of the theory of functions of several complex variables" , M.I.T. (1966) (Translated from Russian) |
Comments
References
| [a1] | R. Remmert, "Funktionentheorie" , 1 , Springer (1984) |
| [a2] | J.B. Conway, "Functions of one complex variable" , Springer (1978) |
Morera theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Morera_theorem&oldid=13238