Chow variety

Chow scheme

An algebraic variety whose points parametrize all algebraic subvarieties of dimension and degree of a projective space .

In the product , where is the dual of the projective space , parametrizing the hyperplanes , one considers the subvariety

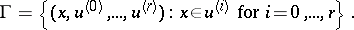Its image 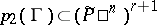under the projection onto the second factor is a hypersurface in 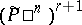which is given by a form in 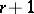systems of 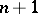variables, homogeneous of degree in each system of variables. The form 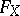is called the associated form (or the Cayley form) of the variety 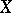. It completely determines as a subvariety. This form was introduced by B.L. van der Waerden and W.L. Chow [1]. The coefficients of 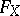are determined up to a constant factor, and are called the Chow coordinates of .

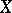The Chow coordinates of a variety 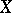determine a point , where is a certain function of 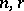and 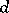. The points 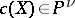corresponding to irreducible subvarieties 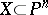of dimension and degree 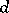form a quasi-projective subvariety 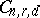, called the Chow variety. If one considers not only the irreducible subvarieties, but also positive algebraic cycles (that is, formal linear combinations of varieties with positive integer coefficients) of dimension and degree 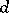in 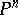, then one obtains a closed subvariety 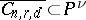, which is also called the Chow variety. The Chow variety is the base of a universal algebraic family 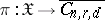, where 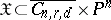, 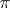is the induced projection, and the fibre 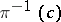above the point 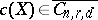is identified with the cycle 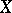. The simplest examples of Chow varieties are the varieties 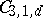of curves of degree 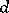in . Thus, 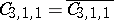is an irreducible variety of dimension 4, isomorphic to the Plücker quadric in ; 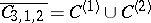consists of two components of dimension 8, where 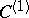corresponds to smooth curves of order two, and 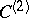to pairs of lines; 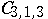consists of four components of dimension 12 corresponding to triplets of lines, curves consisting of a line together with a planar quadric, planar cubics, and non-planar curves of order 3. In all these cases the variety 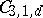is rational. However, it follows from the non-rationality of moduli schemes of curves of sufficiently high genus that for sufficiently high the variety is not rational (cf. [2]).

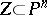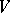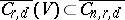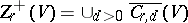If is an algebraic subvariety, then the cycles of dimension and degree that lie in form an algebraic subvariety . This result permits one to introduce a certain algebraic structure on the set of all positive -dimensional cycles on the variety (cf. [1]).

For other approaches to the problem of the classification of varieties cf. Hilbert scheme; Moduli problem.

References

[1]	B.L. van der Waerden, W.L. Chow, "Zur algebraische Geometrie IX" Math. Ann. , 113 (1937) pp. 692–704
[2]	J. Harris, D. Mumford, "On the Kodaira dimension of the moduli space of curves" Invent. Math. , 67 (1982) pp. 23–88
[3]	W.L.V.D. Hodge, "Methods of algebraic geometry" , 2 , Cambridge Univ. Press (1947–1954)
[4]	I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian)

References

[a1]	B. Angéniol, "Familles de cycles algébriques. Schéma de Chow" , Lect. notes in math. , 896 , Springer (1981)