Partially ordered group

A group on which a partial order relation is given such that for all in the inequality implies .

The set in a partially ordered group is called the positive cone, or the integral part, of and satisfies the properties: 1) ; 2) 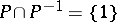; and 3) for all . Any subset of 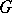that satisfies the conditions 1)–3) induces a partial order on ( 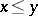if and only if 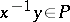) for which 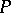is the positive cone.

Examples of partially ordered groups. The additive group of real numbers with the usual order relation; the group 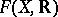of functions from an arbitrary set into 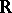, with the operation

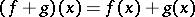and order relation 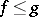if 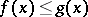for all 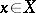; the group of all automorphisms of a totally ordered set 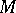with respect to composition of functions, and with order relation if 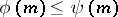for all , where .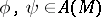

The basic concepts of the theory of partially ordered groups are those of an order homomorphism (cf. Ordered group), a convex subgroup, and Cartesian and lexicographic products.

Important classes of partially ordered groups are totally ordered groups and lattice-ordered groups (cf. Totally ordered group; Lattice-ordered group).

References

[1]	G. Birkhoff, "Lattice theory" , Colloq. Publ. , 25 , Amer. Math. Soc. (1973)
[2]	L. Fuchs, "Partially ordered algebraic systems" , Pergamon (1963)