De Sitter space
complete space-like submanifolds in a
Let  be an
be an 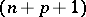 -dimensional Minkowski space of index
-dimensional Minkowski space of index 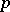 , i.e.,
, i.e.,  and is equipped with the Lorentz metric
and is equipped with the Lorentz metric  . For
. For 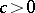 , let
, let
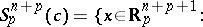 |
 |
Thus, 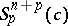 is an
is an  -dimensional indefinite Riemannian manifold of index
-dimensional indefinite Riemannian manifold of index 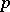 and of constant curvature
and of constant curvature  . It is called an
. It is called an 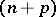 -dimensional de Sitter space of constant curvature
-dimensional de Sitter space of constant curvature  and of index
and of index 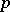 . E. Calabi, S.Y. Cheng and S.T. Yau proved that a complete maximal space-like hypersurface in a Minkowski space
. E. Calabi, S.Y. Cheng and S.T. Yau proved that a complete maximal space-like hypersurface in a Minkowski space 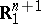 possesses a remarkable Bernstein property. As a generalization of the Bernstein-type problem, S. Ishihara proved that a complete maximal space-like submanifold in a de Sitter space
possesses a remarkable Bernstein property. As a generalization of the Bernstein-type problem, S. Ishihara proved that a complete maximal space-like submanifold in a de Sitter space  is totally geodesic (cf. Totally-geodesic manifold). It was proved by K. Akutagawa [a1], Q.M. Cheng [a2] and K.G. Ramanathan that complete space-like submanifolds with parallel mean curvature vector in a de Sitter space
is totally geodesic (cf. Totally-geodesic manifold). It was proved by K. Akutagawa [a1], Q.M. Cheng [a2] and K.G. Ramanathan that complete space-like submanifolds with parallel mean curvature vector in a de Sitter space  are totally umbilical (cf. also Differential geometry) if
are totally umbilical (cf. also Differential geometry) if
1) 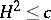 , when
, when 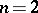 ;
;
2) 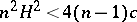 , when
, when 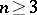 . The conditions 1) and 2) are best possible. When
. The conditions 1) and 2) are best possible. When 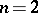 , Akutagawa and Ramanathan constructed many examples of space-like submanifolds in
, Akutagawa and Ramanathan constructed many examples of space-like submanifolds in 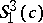 that are not totally umbilical. When
that are not totally umbilical. When 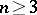 ,
,  , where
, where 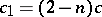 and
and 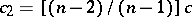 , is a complete space-like hypersurface in
, is a complete space-like hypersurface in 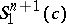 of constant mean curvature
of constant mean curvature 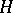 that is not totally umbilical and satisfies
that is not totally umbilical and satisfies 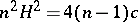 . Cheng gave a characterization of complete non-compact hypersurfaces in
. Cheng gave a characterization of complete non-compact hypersurfaces in 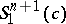 with
with 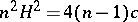 : a complete non-compact hypersurface in
: a complete non-compact hypersurface in 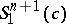 with
with 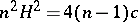 is either isometric to
is either isometric to  or its Ricci curvature is positive and the squared norm of the second fundamental form is a subharmonic function. Therefore, the Cheeger–Gromoll splitting theorem implies that a complete non-compact hypersurface
or its Ricci curvature is positive and the squared norm of the second fundamental form is a subharmonic function. Therefore, the Cheeger–Gromoll splitting theorem implies that a complete non-compact hypersurface 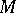 in
in 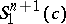 with
with 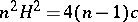 is isometric to
is isometric to  if the number of its ends is not less than
if the number of its ends is not less than  . S. Montiel [a4] has proved that a compact space-like hypersurface in
. S. Montiel [a4] has proved that a compact space-like hypersurface in 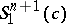 of constant mean curvature is totally umbilical, and Aiyama has generalized this to compact space-like submanifolds in
of constant mean curvature is totally umbilical, and Aiyama has generalized this to compact space-like submanifolds in  with parallel mean curvature vector and flat normal bundle. Complete space-like hypersurfaces in
with parallel mean curvature vector and flat normal bundle. Complete space-like hypersurfaces in 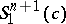 with constant mean curvature have also been characterized under conditions on the squared norm of the second fundamental form.
with constant mean curvature have also been characterized under conditions on the squared norm of the second fundamental form.
Cf. also Anti-de Sitter space.
References
| [a1] | K. Akutagawa, "On space-like hypersurfaces with constant mean curvature in the de Sitter space" Math. Z. , 196 (1987) pp. 13–19 |
| [a2] | Q. M. Cheng, "Complete space-like submanifolds in a de Sitter space with parallel mean curvature vector" Math. Z. , 206 (1991) pp. 333–339 |
| [a3] | Q. M. Cheng, "Hypersurfaces of a Lorentz space form" Arch. Math. , 63 (1994) pp. 271–281 |
| [a4] | S. Montiel, "An integral inequality for compact space-like hypersurfaces in a de Sitter space and application to the case of constant mean curvature" Indiana Univ. Math. J. , 37 (1988) pp. 909–917 |
De Sitter space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=De_Sitter_space&oldid=13196