Kendall coefficient of rank correlation
Kendall 
One of the empirical measures of dependence of two random variables 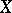 and
and 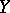 based on ranking the elements of the sample
based on ranking the elements of the sample 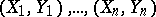 . Thus, the Kendall coefficient is a rank statistic and is defined by the formula
. Thus, the Kendall coefficient is a rank statistic and is defined by the formula
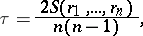 |
where 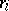 is rank of
is rank of 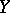 belonging to the pair
belonging to the pair 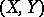 for which the rank of
for which the rank of 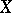 is equal to
is equal to 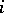 ,
, 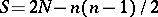 ,
, 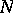 being the number of elements of the sample for which
being the number of elements of the sample for which 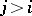 and
and 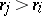 simultaneously. The inequality
simultaneously. The inequality 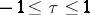 always holds. The Kendall coefficient of rank correlation has been extensively used (see [1]) as an empirical measure of dependence.
always holds. The Kendall coefficient of rank correlation has been extensively used (see [1]) as an empirical measure of dependence.
The Kendall coefficient of rank correlation is applied for testing hypotheses of independence of random variables. If the hypothesis of independence is true, then 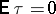 and
and 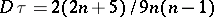 . For small samples
. For small samples 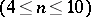 statistical testing of hypotheses of independence is carried out by means of special tables (see [3]). When
statistical testing of hypotheses of independence is carried out by means of special tables (see [3]). When 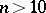 the normal approximation for the distribution of
the normal approximation for the distribution of  is used: If
is used: If
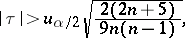 |
then the hypothesis of independence is rejected and the alternative is accepted. Here 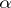 is the significance level, and
is the significance level, and 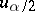 is the
is the 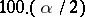 -percent point of the normal distribution. The Kendall coefficient of rank correlation can be used for revealing dependence of two qualitative characteristics, provided that the elements of the sample can be ordered with respect to these characteristics. If
-percent point of the normal distribution. The Kendall coefficient of rank correlation can be used for revealing dependence of two qualitative characteristics, provided that the elements of the sample can be ordered with respect to these characteristics. If 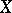 ,
, 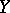 have a joint normal distribution with correlation coefficient
have a joint normal distribution with correlation coefficient 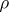 , then its relation to the Kendall coefficient of rank correlation has the form
, then its relation to the Kendall coefficient of rank correlation has the form
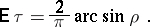 |
See also Spearman coefficient of rank correlation; Rank test.
References
| [1] | M.G. Kendall, "Rank correlation methods" , Griffin (1970) |
| [2] | B.L. van der Waerden, "Mathematische Statistik" , Springer (1957) |
| [3] | L.N. Bol'shev, N.V. Smirnov, "Tables of mathematical statistics" , Libr. math. tables , 46 , Nauka (1983) (In Russian) (Processed by L.S. Bark and E.S. Kedrova) |
| [4] | E.S. Pearson, H.O. Hartley, "Biometrica tables for statisticians" , 1 , Cambridge Univ. Press (1956) |
Kendall coefficient of rank correlation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kendall_coefficient_of_rank_correlation&oldid=13189