Certain special constant Hermitian 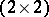 -matrices with complex entries. They were introduced by W. Pauli (1927) to describe spin (
-matrices with complex entries. They were introduced by W. Pauli (1927) to describe spin ( ) and magnetic moment
) and magnetic moment  of an electron. His equation describes correctly in the non-relativistic case particles of spin 1/2 (in units
of an electron. His equation describes correctly in the non-relativistic case particles of spin 1/2 (in units  ) and can be obtained from the Dirac equation for
) and can be obtained from the Dirac equation for 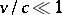 . In explicit form the Pauli matrices are:
. In explicit form the Pauli matrices are:
Their eigen values are 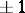 . The Pauli matrices satisfy the following algebraic relations:
. The Pauli matrices satisfy the following algebraic relations:
Together with the unit matrix
the Pauli matrices form a complete system of second-order matrices by which an arbitrary linear operator (matrix) of dimension 2 can be expanded. They act on two-component spin functions 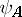 ,
, 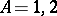 , and are transformed under a rotation of the coordinate system by a linear two-valued representation of the rotation group. Under a rotation by an infinitesimal angle
, and are transformed under a rotation of the coordinate system by a linear two-valued representation of the rotation group. Under a rotation by an infinitesimal angle 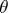 around an axis with a directed unit vector
around an axis with a directed unit vector 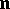 , a spinor
, a spinor 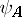 is transformed according to the formula
is transformed according to the formula
From the Pauli matrices one can form the Dirac matrices 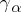 ,
, 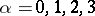 :
:
The real linear combinations of 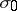 ,
,  ,
, 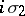 ,
, 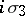 form a four-dimensional subalgebra of the algebra of complex
form a four-dimensional subalgebra of the algebra of complex 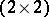 -matrices (under matrix multiplication) that is isomorphic to the simplest system of hypercomplex numbers, the quaternions, cf. Quaternion. They are used whenever an elementary particle has a discrete parameter taking only two values, for example, to describe an isospin nucleon (a proton-neutron). Quite generally, the Pauli matrices are used not only to describe isotopic space, but also in the formalism of the group of inner symmetries
-matrices (under matrix multiplication) that is isomorphic to the simplest system of hypercomplex numbers, the quaternions, cf. Quaternion. They are used whenever an elementary particle has a discrete parameter taking only two values, for example, to describe an isospin nucleon (a proton-neutron). Quite generally, the Pauli matrices are used not only to describe isotopic space, but also in the formalism of the group of inner symmetries 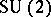 . In this case they are generators of a
. In this case they are generators of a  -dimensional representation of
-dimensional representation of  and are denoted by
and are denoted by 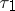 ,
,  and
and 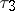 . Sometimes it is convenient to use the linear combinations
. Sometimes it is convenient to use the linear combinations
In certain cases one introduces for a relativistically covariant description of two-component spinor functions instead of the Pauli matrices, matrices 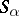 related by means of the following identities:
related by means of the following identities:
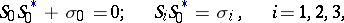 | (1) |
where the symbol  denotes complex conjugation. The matrices
denotes complex conjugation. The matrices 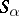 satisfy the commutator relations
satisfy the commutator relations
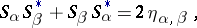 | (2) |
where 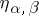 are the components of the metric tensor of the Minkowski space of signature
are the components of the metric tensor of the Minkowski space of signature 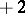 . The formulas (1) and (2) make it possible to generalize the Pauli matrices covariantly to an arbitrary curved space:
. The formulas (1) and (2) make it possible to generalize the Pauli matrices covariantly to an arbitrary curved space:
where 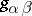 are the components of the metric tensor of the curved space.
are the components of the metric tensor of the curved space.
References
| [1] | W. Pauli, , Works on quantum theory , 1–2 , Moscow (1975–1977) (In Russian; translated from German) |
| [2] | N.F. Nelina, "Physics of elementary particles" , Moscow (1977) (In Russian) |
| [3] | D. Bril, J.A. Wheeler, , The latest problems on gravitation , Moscow (1961) pp. 381–427 (In Russian) |
References
| [a1] | W. Pauli, "Zur Quantenmechanik des magnetischen Elektrons" Z. Phys. , 43 : 601 |
| [a2] | W. Pauli (ed.) , Handbuch der Physik , 24 , Springer (1933) |
| [a3] | R.M. Wald, "General relativity" , Univ. Chicago Press (1984) pp. Chapt. 4 |
| [a4] | Y. Choquet-Bruhat, C. DeWitt-Morette, M. Dillard-Bleick, "Analysis, manifolds and physics" , North-Holland (1982) (Translated from French) |
How to Cite This Entry:
Pauli matrices. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pauli_matrices&oldid=13182
This article was adapted from an original article by V.G. Krechet (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article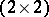 -matrices with complex entries. They were introduced by W. Pauli (1927) to describe spin (
-matrices with complex entries. They were introduced by W. Pauli (1927) to describe spin ( ) and magnetic moment
) and magnetic moment  of an electron. His equation describes correctly in the non-relativistic case particles of spin 1/2 (in units
of an electron. His equation describes correctly in the non-relativistic case particles of spin 1/2 (in units  ) and can be obtained from the Dirac equation for
) and can be obtained from the Dirac equation for 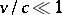 . In explicit form the Pauli matrices are:
. In explicit form the Pauli matrices are:
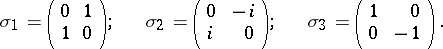
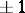 . The Pauli matrices satisfy the following algebraic relations:
. The Pauli matrices satisfy the following algebraic relations:
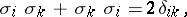
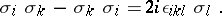
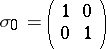
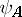 ,
, 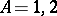 , and are transformed under a rotation of the coordinate system by a linear two-valued representation of the rotation group. Under a rotation by an infinitesimal angle
, and are transformed under a rotation of the coordinate system by a linear two-valued representation of the rotation group. Under a rotation by an infinitesimal angle 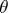 around an axis with a directed unit vector
around an axis with a directed unit vector 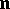 , a spinor
, a spinor 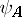 is transformed according to the formula
is transformed according to the formula
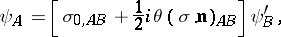
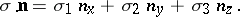
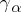 ,
, 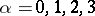 :
:
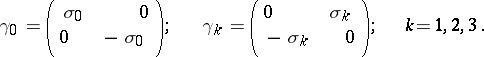
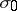 ,
,  ,
, 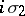 ,
, 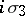 form a four-dimensional subalgebra of the algebra of complex
form a four-dimensional subalgebra of the algebra of complex 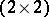 -matrices (under matrix multiplication) that is isomorphic to the simplest system of hypercomplex numbers, the quaternions, cf. Quaternion. They are used whenever an elementary particle has a discrete parameter taking only two values, for example, to describe an isospin nucleon (a proton-neutron). Quite generally, the Pauli matrices are used not only to describe isotopic space, but also in the formalism of the group of inner symmetries
-matrices (under matrix multiplication) that is isomorphic to the simplest system of hypercomplex numbers, the quaternions, cf. Quaternion. They are used whenever an elementary particle has a discrete parameter taking only two values, for example, to describe an isospin nucleon (a proton-neutron). Quite generally, the Pauli matrices are used not only to describe isotopic space, but also in the formalism of the group of inner symmetries 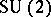 . In this case they are generators of a
. In this case they are generators of a  -dimensional representation of
-dimensional representation of  and are denoted by
and are denoted by 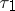 ,
,  and
and 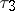 . Sometimes it is convenient to use the linear combinations
. Sometimes it is convenient to use the linear combinations
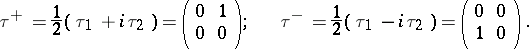
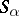 related by means of the following identities:
related by means of the following identities:
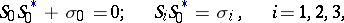
 denotes complex conjugation. The matrices
denotes complex conjugation. The matrices 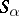 satisfy the commutator relations
satisfy the commutator relations
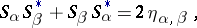
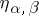 are the components of the metric tensor of the Minkowski space of signature
are the components of the metric tensor of the Minkowski space of signature 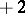 . The formulas (1) and (2) make it possible to generalize the Pauli matrices covariantly to an arbitrary curved space:
. The formulas (1) and (2) make it possible to generalize the Pauli matrices covariantly to an arbitrary curved space:
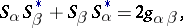
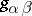 are the components of the metric tensor of the curved space.
are the components of the metric tensor of the curved space.