Minimal set

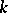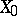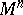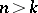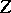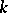A minimal set in a Riemannian space is a generalization of a minimal surface. A minimal set is a -dimensional closed subset in a Riemannian space , , such that for some subset of -dimensional Hausdorff measure zero the set 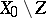is a differentiable 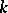-dimensional minimal surface (that is, is an extremum of the 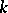-dimensional volume functional 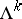, defined on 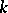-dimensional surfaces imbedded in 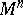). The notion of a "minimal set" amalgamates several mathematical ideas called upon to serve in the so-called multi-dimensional Plateau problem (cf. also Plateau problem, multi-dimensional).

A.T. Fomenko

A minimal set in a topological dynamical system 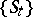is a non-empty closed invariant (that is, consisting wholly of trajectories) subset 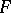of the phase space 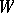of the system which does not have proper closed invariant subsets. The latter is equivalent to saying that each trajectory in 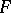is everywhere dense in 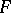. The notion of a minimal set was introduced by G.D. Birkhoff (see [1]) for the case of a flow (the "time" 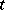running through the real numbers). 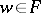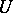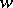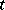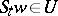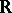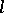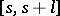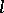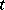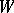He proved (see [1], [2]) that if is a compact minimal set and , then for any neighbourhood of the set of those for which is relatively dense in (that is, there is an such that in each "time interval" of length there is at least one with ); conversely, if is a complete metric space and a point 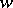has the above property, then the closure of its trajectory 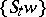is a compact minimal set (the same is true for a cascade; regarding more general groups of transformations see, for example, [3] and [4]). Birkhoff called this property of (and its trajectory) recurrence; another terminology, suggested by W.H. Gottschalk and G.A. Hedlund [3], is also used, in which this property is called almost-periodicity of the point 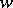. If , then the dynamical system itself is called minimal.

If a trajectory has compact closure, then it contains a minimal set 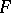(for semi-groups of continuous transformations 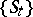, with non-negative real or integer 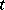, an analogue of this result holds, where in 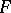the transformations 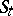are even invertible [5]). However, research into the limit behaviour of the trajectories of a dynamical system does not reduce to the study of only the minimal sets of the latter. A minimal set of a smooth flow of class 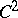on a two-dimensional closed surface 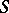has a very simple structure: it is either a point, a closed trajectory or the whole surface, which is then a torus (Schwarz's theorem, [6]). In the general case the structure of a minimal set can be very complicated (in this connection, in addition to what is said in [2]–[4] it must be said that minimality of a dynamical system places no restrictions on its ergodic properties with respect to any of its invariant measures, [7]). Minimal sets are the fundamental objects of study in topological dynamics.

References

[1]	G.D. Birkhoff, "Dynamical systems" , Amer. Math. Soc. (1927)
[2]	V.V. Nemytskii, V.V. Stepanov, "Qualitative theory of differential equations" , Princeton Univ. Press (1960) (Translated from Russian)
[3]	W.H. Gottschalk, G.A. Hedlund, "Topological dynamics" , Amer. Math. Soc. (1955)
[4]	I.U. Bronshtein, "Extensions of minimal transformation groups" , Sijthoff & Noordhoff (1979) (Translated from Russian)
[5]	B.M. Levitan, V.V. Zhikov, "Almost-periodic functions and differential equations" , Cambridge Univ. Press (1982) (Translated from Russian)
[6]	P. Hartman, "Ordinary differential equations" , Wiley (1964)
[7]	A.B. Katok, Ya.G. Sinai, A.M. Stepin, "Theory of dynamical systems and general transformation groups with invariant measure" J. Soviet Math. , 7 (1977) pp. 974–1065 Itogi. Nauk. i Tekhn. Mat. Anal. , 13 (1975) pp. 129–262

D.V. Anosov

Comments

The terminology around the notions of recurrence and almost periodicity of points in a topological dynamical system is confusing. These are two mainstreams of nomenclature, represented by [1], [2], [a8] on the one hand, and by [3], [a1], [a2] on the other. The type of point mentioned above, namely, a point 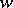such that for every neighbourhood 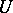of 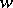the set 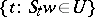is relatively dense in , is called almost periodic in [3], [4], [a1], [a2], and almost recurrent in [2] and [a8]. (In [2], [a8], almost periodicity has another meaning.) Formally, the notion of a recurrent point as defined in [1], [2], [a8] is different: see Recurrent point; a recurrent point is always [3]-almost periodic (i.e., almost-recurrent), but not conversely. In a dynamical system on a complete metric space the two notions coincide. (In [3] the notion of a recurrent point is used in the meaning of "positively and negatively Poisson stable" .) What Birkhoff proved was the equivalence of recurrence of a point 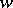(according to the terminology of [1], [2]) and the property that has a compact minimal orbit closure, provided the phase space is a complete metric space. Using the terminology of [3] one can show: If 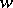has a compact minimal orbit closure, the 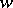is an almost-periodic point (no conditions on the phase space); conversely, an almost-periodic point has a minimal orbit closure, which is compact if the phase space is locally compact and Hausdorff (no metrizability assumed).

The classification of compact minimal sets in topological dynamics is a largely unsolved problem. Only for special classes something can be said (cf. Distal dynamical system); see [4], [a2] and [a1]. Unsolved is also the problem as to which (compact) Hausdorff spaces can be the phase space of a minimal flow or a minimal cascade. In this respect, Schwarz's theorem, mentioned above, gives a partial solution for compact surfaces; for a generalization, see [a4]. A Klein bottle cannot be minimal under a continuous flow (the Kneser theorem, see also [a6]), neither can the real projective plane (see [a5]). Still open is Gottschalk's conjecture (a particular case of Seifert's conjecture): 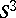cannot be the phase space of a minimal flow; see Appendix II of [a7] for references (the Seifert conjecture states that any smooth flow on 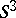has a periodic orbit; there is a 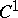-counterexample, [a9]). For results about cascades, see [a3], [a10].

References

[a1]	J. Auslander, "Minimal flows and their extensions" , North-Holland (1988)
[a2]	R. Ellis, "Lectures on topological dynamics" , Benjamin (1969)
[a3]	G. Glasner, B. Weiss, "On the construction of minimal skew products" Israel J. Math. , 34 (1979) pp. 321–336
[a4]	C. Gutierrez, "Smoothing continuous flows on two-manifolds and recurrences" Ergod. Th. Dynam. Sys. , 6 (1986) pp. 17–44
[a5]	P.-F. Lam, "Inverses of recurrent and periodic points under homomorphisms of dynamical systems" Math. Systems Theory , 6 (1972) pp. 26–36
[a6]	N.G. Markley, "The Poincaré–Bendixson theorem for the Klein bottle" Trans. Amer. Math. Soc. , 135 (1969) pp. 159–165
[a7]	L. Markus, "Lectures in differentiable dynamics" , Amer. Math. Soc. (1980) pp. Appendix II
[a8]	K.S. Sibirskii, "Introduction to topological dynamics" , Noordhoff (1975) (Translated from Russian)
[a9]	P.A. Schweitzer, "Counterexamples to the Seifert conjecture and opening closed leaves of foliations" Amer. of Math. (2) , 100 (1974) pp. 386–400
[a10]	A. Fahti, M. Herman, "Existence de diffeomorphismes minimaux" Astérisque , 49 (1977) pp. 37–59