Independent functions, system of

A sequence of measurable functions 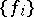such that

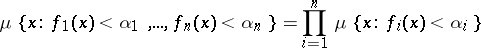for any and any . The simplest example of a system of independent functions is the Rademacher system.

(Kolmogorov's) criterion for the almost-everywhere convergence of a series of independent functions: For a series of independent functions 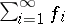to converge almost everywhere it is necessary and sufficient that for some 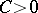the following three series converge:

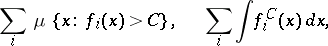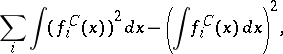where

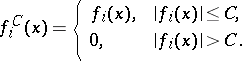Comments

Of course, to be able to introduce the concept of a system of independent functions one needs to have a measure space 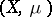on which the functions are defined and measurable (with respect to 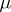). Moreover, 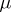must be positive and finite, so 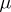can be taken a probability measure (then 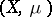is a probability space). An example is .

In this abstract setting, instead of functions one takes random variables, thus obtaining a system of independent random variables.

The notion of a system of independent functions (random variables) should not be mixed up with that of an independent set of elements of a vector space 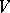over a field 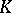: A set of elements 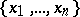in 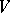such that for 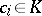, 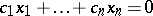implies 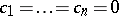, see also Vector space.

References

[a1]	J.-P. Kahane, "Some random series of functions" , Cambridge Univ. Press (1985)