Closure of a set

in a topological space

The intersection of all closed sets (cf. Closed set) containing the set.

Comments

In the Russian literature the closure of a set is denoted by , or to express that the closure is taken in the space , in the Western literature one uses , , , or .

Another definition of closure is as follows. The closure of in is the set of all satisfying: Every neighbourhood of intersects .

The closure operation satisfies: 1) ; 2) ; 3) ; and 4) 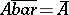. Any operation satisfying 1), 2), 3), and 4) is called a closure operation. One can define a topological space by means of a closure operation: The closed sets are to be those sets that equal their own closure.

This approach is taken in [a1].

References

[a1]	K. Kuratowski, "Topology" , 1 , PWN & Acad. Press (1966) (Translated from French)