Linearly-disjoint extensions
of a field 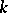
Two subextensions 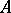 and
and 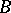 of an extension
of an extension  of
of 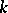 such that the subalgebra generated by
such that the subalgebra generated by 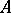 and
and 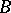 in
in  is (isomorphic to) the tensor product
is (isomorphic to) the tensor product 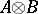 over
over 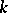 (cf. Extension of a field). Let
(cf. Extension of a field). Let 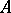 and
and 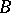 be arbitrary subrings of an extension
be arbitrary subrings of an extension  of
of 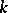 , containing
, containing 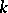 , and let
, and let 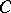 be the subring of
be the subring of  generated by
generated by 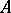 and
and 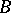 . There is always a ring homomorphism
. There is always a ring homomorphism 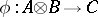 that associates with an element
that associates with an element 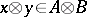 ,
, 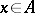 ,
, 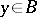 , the product
, the product 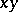 in
in 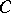 . The algebras
. The algebras 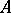 and
and 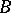 are said to be linearly disjoint over
are said to be linearly disjoint over 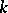 if
if 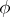 is an isomorphism of
is an isomorphism of 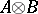 onto
onto 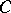 . In this case,
. In this case, 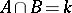 . For
. For 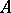 and
and 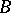 to be linearly disjoint over
to be linearly disjoint over 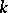 it is sufficient that there is a basis of
it is sufficient that there is a basis of 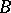 over
over 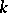 that is independent over
that is independent over 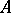 . If
. If 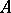 is a finite extension of
is a finite extension of 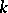 , then the degree of the extension
, then the degree of the extension 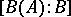 does not exceed the degree of extension
does not exceed the degree of extension 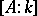 and equality holds if and only if
and equality holds if and only if  and
and 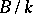 are linearly disjoint.
are linearly disjoint.
References
| [1] | N. Bourbaki, "Algebra" , Elements of mathematics , 1 , Springer (1988) pp. Chapts. 4–7 (Translated from French) |
Comments
References
| [a1] | O. Zariski, P. Samuel, "Commutative algebra" , 1 , Springer (1975) |
Linearly-disjoint extensions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Linearly-disjoint_extensions&oldid=13138