Elementary theory
A collection of closed formulas of first-order predicate logic. The elementary theory 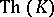 of a class
of a class 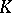 of algebraic systems (cf. Algebraic system) of signature
of algebraic systems (cf. Algebraic system) of signature  is defined to be the collection of all closed formulas of the first-order predicate logic of signature
is defined to be the collection of all closed formulas of the first-order predicate logic of signature  that are true in all systems of
that are true in all systems of 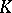 . If
. If  consists of a single system
consists of a single system 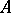 , then the elementary theory of the class
, then the elementary theory of the class 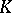 is the elementary theory of the system
is the elementary theory of the system 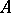 . Two algebraic systems of the same signature are said to be elementarily equivalent if their elementary theories are the same. An algebraic system
. Two algebraic systems of the same signature are said to be elementarily equivalent if their elementary theories are the same. An algebraic system 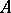 of signature
of signature  is called a model of an elementary theory
is called a model of an elementary theory 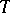 of signature
of signature  if all formulas of
if all formulas of 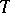 are true in
are true in 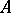 . An elementary theory is called consistent if it has models. A consistent elementary theory is called complete if any two models of it are elementarily equivalent. The class of all models of an elementary theory
. An elementary theory is called consistent if it has models. A consistent elementary theory is called complete if any two models of it are elementarily equivalent. The class of all models of an elementary theory 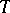 is denoted by
is denoted by 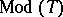 . An elementary theory
. An elementary theory 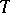 is called solvable (or decidable) if the set of formulas
is called solvable (or decidable) if the set of formulas 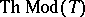 (that is, the set of all logical consequences of
(that is, the set of all logical consequences of 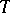 ) is recursive. A class
) is recursive. A class 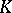 of algebraic systems of signature
of algebraic systems of signature  is called axiomatizable if there exists an elementary theory
is called axiomatizable if there exists an elementary theory 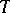 of signature
of signature  such that
such that 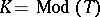 . In this case
. In this case 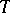 is called a collection of axioms for
is called a collection of axioms for 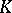 . A class
. A class 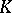 is axiomatizable if and only if
is axiomatizable if and only if 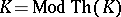 . For example, the class of dense linear orders without a smallest or largest element is axiomatizable, its elementary theory is solvable and any two systems of this class are elementarily equivalent, since the elementary theory of this class is complete; moreover, its elementary theory is finitely axiomatizable. The class of finite cyclic groups is not axiomatizable; however, its elementary theory is solvable, and hence recursively axiomatizable. There are examples of finitely-axiomatizable unsolvable elementary theories. They include those of groups, rings, fields, and others. However, a complete recursively-axiomatizable elementary theory is necessarily solvable. Therefore, to prove the solvability of a recursively-axiomatizable elementary theory it is sufficient to observe that it is complete.
. For example, the class of dense linear orders without a smallest or largest element is axiomatizable, its elementary theory is solvable and any two systems of this class are elementarily equivalent, since the elementary theory of this class is complete; moreover, its elementary theory is finitely axiomatizable. The class of finite cyclic groups is not axiomatizable; however, its elementary theory is solvable, and hence recursively axiomatizable. There are examples of finitely-axiomatizable unsolvable elementary theories. They include those of groups, rings, fields, and others. However, a complete recursively-axiomatizable elementary theory is necessarily solvable. Therefore, to prove the solvability of a recursively-axiomatizable elementary theory it is sufficient to observe that it is complete.
Several methods for proving completeness are known. An elementary theory is called categorical in cardinality 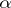 (cf. Categoricity in cardinality) if all its models of cardinality
(cf. Categoricity in cardinality) if all its models of cardinality 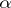 are isomorphic. An elementary theory that is categorical in some infinite cardinality and has no finite models is necessarily complete. For example, the elementary theory of algebraically closed fields of a given characteristic is recursively axiomatizable and categorical in every uncountable cardinality; it has no finite models, and therefore it is complete and solvable. In particular, the elementary theory of the field of complex numbers is solvable. Two formulas in the same signature as that of a theory
are isomorphic. An elementary theory that is categorical in some infinite cardinality and has no finite models is necessarily complete. For example, the elementary theory of algebraically closed fields of a given characteristic is recursively axiomatizable and categorical in every uncountable cardinality; it has no finite models, and therefore it is complete and solvable. In particular, the elementary theory of the field of complex numbers is solvable. Two formulas in the same signature as that of a theory 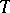 are equivalent in the theory
are equivalent in the theory 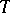 if they contain the same variables and if, for any model
if they contain the same variables and if, for any model 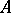 of
of 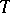 and any assignment of elements of
and any assignment of elements of 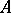 to their free variables, the formulas are either both true or both false. A complete elementary theory
to their free variables, the formulas are either both true or both false. A complete elementary theory 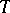 of finite or countable signature is countably categorical if and only if for every
of finite or countable signature is countably categorical if and only if for every  there are finitely many formulas with
there are finitely many formulas with  free variables
free variables  such that every formula of the appropriate signature with
such that every formula of the appropriate signature with  as free variables is equivalent in
as free variables is equivalent in  to one of those formulas. A complete theory of finite or countable signature that is categorical in one uncountable cardinality is also categorical in every other uncountable cardinality. A system
to one of those formulas. A complete theory of finite or countable signature that is categorical in one uncountable cardinality is also categorical in every other uncountable cardinality. A system 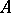 of signature
of signature  is called an elementary subsystem of a system
is called an elementary subsystem of a system 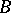 of the same signature if
of the same signature if  is a subsystem of
is a subsystem of 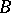 and if for every formula
and if for every formula 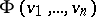 of the first-order predicate logic of
of the first-order predicate logic of  with free variables
with free variables  and all
and all 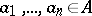 , the truth of
, the truth of 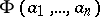 in
in 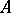 implies its truth in
implies its truth in 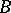 . An elementary theory
. An elementary theory  is called model complete if for any two models
is called model complete if for any two models 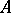 and
and 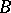 of it the fact that
of it the fact that 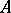 is a subsystem of
is a subsystem of  implies that it is an elementary subsystem. It turns out that a model-complete theory having a model that can be isomorphically imbedded in every model of the theory is complete. Two systems of the same signature which satisfy the same prenex formulas without existential quantifiers are called universally equivalent. A model-complete elementary theory all models of which are universally equivalent is complete. Using the technique of model completeness one can prove that real-closed fields, in particular, the field of real numbers, have a complete and solvable elementary theory. Among the other solvable elementary theories are those of addition of natural numbers and integers, of Abelian groups, of
implies that it is an elementary subsystem. It turns out that a model-complete theory having a model that can be isomorphically imbedded in every model of the theory is complete. Two systems of the same signature which satisfy the same prenex formulas without existential quantifiers are called universally equivalent. A model-complete elementary theory all models of which are universally equivalent is complete. Using the technique of model completeness one can prove that real-closed fields, in particular, the field of real numbers, have a complete and solvable elementary theory. Among the other solvable elementary theories are those of addition of natural numbers and integers, of Abelian groups, of 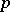 -adic number fields, of finite fields, of residue class fields, of ordered Abelian groups, and of Boolean algebras.
-adic number fields, of finite fields, of residue class fields, of ordered Abelian groups, and of Boolean algebras.
The general study of unsolvable elementary theories was initiated by A. Tarski in the 1940s, but even earlier, in 1936, A. Church had proved the unsolvability of first-order predicate logic and J. Rosser, also in 1936, had proved the unsolvability of the arithmetic of the natural numbers. The elementary theory  of a class
of a class 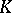 of algebraic systems of the same signature
of algebraic systems of the same signature  is said to be inseparable if there is no recursive set of formulas containing
is said to be inseparable if there is no recursive set of formulas containing 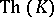 and not containing any closed formula which is false in all systems in
and not containing any closed formula which is false in all systems in  . The elementary theory of a class
. The elementary theory of a class 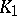 of systems of signature
of systems of signature 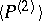 consisting of a single two-place predicate is called relatively definable in the elementary theory of a class
consisting of a single two-place predicate is called relatively definable in the elementary theory of a class 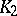 of systems of signature
of systems of signature 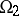 if there exist formulas
if there exist formulas 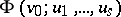 and
and 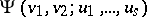 of
of 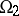 such that for every system
such that for every system 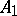 in
in 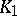 one can find a system
one can find a system 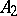 in
in 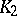 and elements
and elements 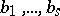 in
in  for which the set
for which the set  together with the predicate
together with the predicate  , defined on
, defined on 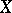 so that
so that 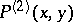 is true if and only if
is true if and only if  is true in
is true in 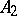 , forms an algebraic system isomorphic to
, forms an algebraic system isomorphic to  . This definition extends naturally to the theory of classes
. This definition extends naturally to the theory of classes 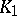 of arbitrary signature. If the elementary theory of a class
of arbitrary signature. If the elementary theory of a class 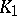 is inseparable and relatively definable in the elementary theory of a class
is inseparable and relatively definable in the elementary theory of a class 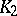 , then that of
, then that of  is also inseparable. This makes it possible to prove that the elementary theories of many classes of algebraic systems are inseparable. Here it is convenient to take as
is also inseparable. This makes it possible to prove that the elementary theories of many classes of algebraic systems are inseparable. Here it is convenient to take as 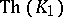 the elementary theory of all finite binary relations or that of all finite symmetric relations, or similar elementary theories. Inseparable elementary theories are unsolvable. So are those of the field of rational numbers and of many classes of rings and fields. The unsolvability of the elementary theory of finite groups is an important result of A.I. Mal'tsev.
the elementary theory of all finite binary relations or that of all finite symmetric relations, or similar elementary theories. Inseparable elementary theories are unsolvable. So are those of the field of rational numbers and of many classes of rings and fields. The unsolvability of the elementary theory of finite groups is an important result of A.I. Mal'tsev.
References
| [1] | Yu.L. Ershov, I.A. Lavrov, A.D. Taimanov, M.A. Taitslin, "Elementary theories" Uspekhi Mat. Nauk , 20 : 4 (1965) pp. 37–108 (In Russian) |
| [2] | Yu.L. Ershov, "Decision problems and constructivizable models" , Moscow (1980) (In Russian) |
Comments
Somewhat more generally one defines recursive separability and inseparability for pairs of theories rather than for a single theory. Thus, two disjoint sets of natural numbers  and
and 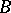 are said to be recursively separable if there exists a recursive set
are said to be recursively separable if there exists a recursive set  containing
containing 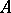 which is disjoint from
which is disjoint from 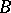 . This is a symmetric notion. The sets
. This is a symmetric notion. The sets 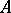 and
and 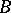 are (recursively) inseparable if they are not recursively separable. The single theory definition of inseparability results if this is applied to the sets
are (recursively) inseparable if they are not recursively separable. The single theory definition of inseparability results if this is applied to the sets 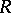 and
and  of refutable and provable formulas, or rather their associated sets of Gödel numbers
of refutable and provable formulas, or rather their associated sets of Gödel numbers 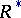 and
and 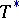 .
.
References
| [a1] | C.C. Chang, H.J. Keisler, "Model theory" , North-Holland (1973) |
| [a2] | R.M. Smullyan, "Theory of formal systems" , Princeton Univ. Press (1961) pp. Chapt. III |
Elementary theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Elementary_theory&oldid=13131