Non-singular boundary point
regular boundary point
An accessible boundary point (cf. Attainable boundary point)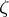 
of the domain of definition 
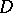of a single-valued analytic function 
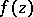of a complex variable 
such that 
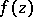has an analytic continuation to 
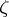along any path inside 
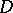to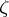 
. In other words, a non-singular boundary point is accessible, but not singular. See also Singular point of an analytic function.
Comments
Note that the same point in the boundary of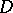 
may give rise to several different accessible boundary points, some of which may be singular, others regular. E.g., consider the domain 
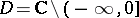, and the function 
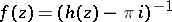, where 
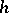is the principal value of 
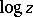. Then "above" 
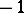there are two accessible boundary points: one singular, corresponding to approach along 
, 
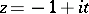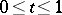; one regular, corresponding to approach along 
, 
.
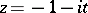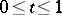References
| [a1] | A.I. Markushevich, "Theory of functions of a complex variable" , 3 , Chelsea (1977) pp. Chapts. 2; 8 (Translated from Russian) |
Non-singular boundary point. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Non-singular_boundary_point&oldid=13119