Hilbert scheme

A construction in algebraic geometry by means of which a set of closed subvarieties of a projective space with a given Hilbert polynomial can be endowed with the structure of an algebraic variety. More precisely, let 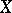be a projective scheme over a locally Noetherian scheme 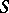and let 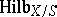be the functor assigning to each 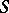-scheme 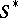the set of closed subschemes 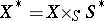which are flat over 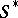. The functor 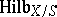can be represented locally as a Noetherian scheme, known as the Hilbert scheme of 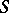-schemes of 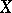, and is denoted by 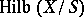[4]. By the definition of a representable functor, for any 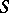-scheme 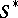there is a bijection 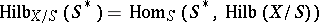. In particular, if 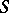is the spectrum of a field 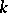(cf. Spectrum of a ring) and 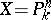is a projective space over 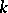, then the set of rational 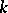-points of 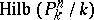is in one-to-one correspondence with the set of closed subvarieties in .

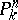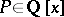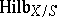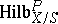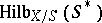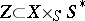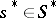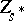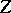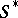For any polynomial with rational coefficients the functor contains a subfunctor which isolates in the set the subset of subschemes such that for any point the fibre of the projection of on has 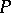as its Hilbert polynomial. The functor 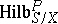can be represented by the Hilbert scheme 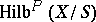, which is projective over 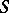. The scheme 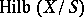is the direct sum of the schemes 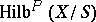over all 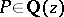. For any connected ground scheme 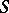the scheme 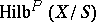is also connected [2].

References

[1]	D. Mumford, "Lectures on curves on an algebraic surface" , Princeton Univ. Press (1966)
[2]	D. Mumford, "Geometric invariant theory" , Springer (1965)
[3]	A. Grothendieck, "Techniques de construction et théorèmes d'existence en géométrie algébrique, IV: Les schémas de Hillbert" , Sem. Bourbaki , 13 : 221 (1960–1961)
[4]	R. Hartshorne, "Connectedness of the Hilbert scheme" Publ. Math. IHES , 29 (1966) pp. 5–48
[5]	I.V. Dolgachev, "Abstract algebraic geometry" J. Soviet Math. , 2 : 3 (1974) pp. 264–303 Itogi Nauk. i Tekhn. Algebra Topol. Geom. , 10 (1972) pp. 47–112