Canonical class
The class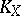 
of divisors, with respect to linear equivalence on an algebraic variety 
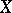, which are divisors of differential forms 
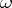of maximal degree. If 
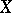is a non-singular algebraic variety and 
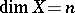, then in local coordinates 
a form 
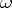can be written as
 |
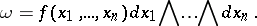The divisor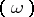 
of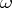 
is locally equal to the divisor 
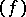of this rational function 
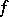. This construction does not depend on the choice of local coordinates and gives the divisor 
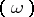of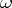 
on all of 
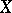. Since for any other form 
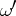of the same degree as 
, 
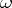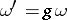, it follows that 
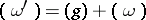, and corresponding divisors are equivalent. The canonical class 
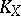thus constructed is the first Chern class of the sheaf 
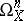of regular differential forms of degree 
. Its numerical characteristics (degree, index, self-intersections, etc.) are effectively calculable invariants of the algebraic variety.
If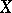 
is a non-singular projective curve of genus 
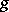, then 
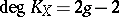. For elliptic curves and, more generally, for Abelian varieties, 
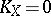. If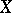 
is a non-singular hypersurface of degree 
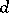in projective space 
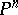, then 
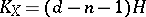, where 
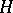is a hyperplane section of it.
See also Canonical imbedding.
References
| [1] | I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) |
Comments
References
| [a1] | S. Iitaka, "Algebraic geometry, an introduction to birational geometry of algebraic varieties" , Springer (1982) |
Canonical class. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Canonical_class&oldid=13082