Hermite equation

A linear homogeneous second-order ordinary differential equation

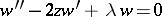or, in self-adjoint form,

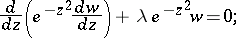here 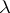is a constant. The change of the unknown function 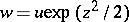transforms the Hermite equation into

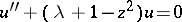and after the change of variables

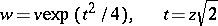one obtains from the Hermite equation the Weber equation

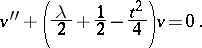For 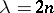, where is a natural number, the Hermite equation has among its solutions the Hermite polynomial of degree (cf. Hermite polynomials),

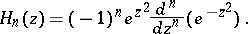This explains the name of the differential equation. In general, the solutions of the Hermite equation can be expressed in terms of special functions: the parabolic cylinder functions or Weber–Hermite functions.

References

[a1]	E.T. Whittaker, G.N. Watson, "A course of modern analysis" , Cambridge Univ. Press (1965)