Arveson spectrum
Suppose, for initial discussion, that the unit circle 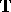 is represented by a strongly continuous, isometric representation
is represented by a strongly continuous, isometric representation 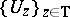 on a Banach space
on a Banach space 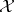 (cf. also Representation theory). The space
(cf. also Representation theory). The space 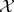 may be quite arbitrary, but for definiteness, consider
may be quite arbitrary, but for definiteness, consider  to be any Banach space of functions on
to be any Banach space of functions on 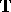 on which translation is continuous and then take translation for
on which translation is continuous and then take translation for 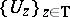 . For
. For 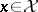 and an integer
and an integer  , let
, let 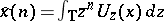 , where the integral is a vector-valued Riemann integral. Then
, where the integral is a vector-valued Riemann integral. Then 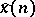 is an element of
is an element of 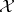 that satisfies the equation
that satisfies the equation 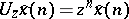 ,
, 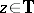 . Thus,
. Thus, 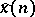 is a common eigenvector for all the operators
is a common eigenvector for all the operators 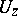 . If
. If 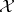 is a Banach function space, then
is a Banach function space, then  , as a function, is the
, as a function, is the  th Fourier coefficient of
th Fourier coefficient of  multiplied by the function
multiplied by the function 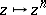 . The spectrum of
. The spectrum of  is defined to be
is defined to be 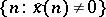 and is denoted by
and is denoted by 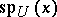 . Thus, the spectrum generalizes the idea of the support of the Fourier transform (i.e. Fourier series) of a function. It can be shown that
. Thus, the spectrum generalizes the idea of the support of the Fourier transform (i.e. Fourier series) of a function. It can be shown that  is non-empty precisely when
is non-empty precisely when 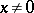 ; in fact, the series
; in fact, the series 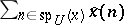 is
is 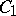 -summable to
-summable to  (cf. also Summation methods; Cesàro summation methods). Indeed, the
(cf. also Summation methods; Cesàro summation methods). Indeed, the  th arithmetic mean of the partial sums of this series is given by the vector-valued integral
th arithmetic mean of the partial sums of this series is given by the vector-valued integral 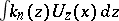 , where
, where 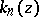 is the Fejér kernel (cf. also Fejér singular integral), and the standard argument using this kernel that shows that the Cesàro means of the Fourier series of a continuous function converge uniformly to the function applies here, mutatis-mutandis, [a7]. Thus, each element of
is the Fejér kernel (cf. also Fejér singular integral), and the standard argument using this kernel that shows that the Cesàro means of the Fourier series of a continuous function converge uniformly to the function applies here, mutatis-mutandis, [a7]. Thus, each element of 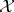 may be reconstructed from its spectral parts just as ordinary functions on
may be reconstructed from its spectral parts just as ordinary functions on 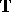 coming from spaces on which translation is continuous may be reconstructed from its Fourier series.
coming from spaces on which translation is continuous may be reconstructed from its Fourier series.
Building on a long tradition of harmonic analysis that may be traced back to [a6] and [a3], W. Arveson [a1] generalized and expanded the analysis just presented to cover cases when an arbitrary locally compact Abelian group 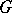 is represented by invertible operators
is represented by invertible operators 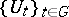 acting on a Banach space
acting on a Banach space 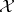 such that
such that 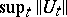 is finite. The assumption of continuity is also weakened. His primary applications concern the settings where:
is finite. The assumption of continuity is also weakened. His primary applications concern the settings where:
a) 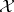 is a Hilbert space and
is a Hilbert space and 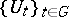 is a strongly continuous unitary representation;
is a strongly continuous unitary representation;
b)  is a
is a 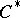 -algebra and
-algebra and 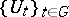 is a strongly continuous representation of
is a strongly continuous representation of 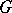 as a group of automorphisms; and
as a group of automorphisms; and
c) 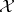 is a von Neumann algebra and
is a von Neumann algebra and 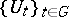 is a representation of
is a representation of 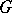 as a group of automorphisms that is continuous with respect to the ultraweak topology on
as a group of automorphisms that is continuous with respect to the ultraweak topology on 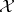 . Since these groups are isometric, in this discussion it is assumed that
. Since these groups are isometric, in this discussion it is assumed that 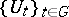 is isometric (cf. also Isometric mapping).
is isometric (cf. also Isometric mapping).
Arveson considers pairs of Banach spaces  that are in duality via a pairing
that are in duality via a pairing 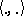 . He assumes that
. He assumes that 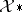 determines the norm on
determines the norm on 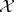 in the sense that
in the sense that
 |
Further, calling the topology on 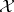 determined by
determined by  the weak topology, he assumes that the weakly closed convex hull of every weakly compact set in
the weak topology, he assumes that the weakly closed convex hull of every weakly compact set in  is weakly compact. These hypotheses guarantee that if
is weakly compact. These hypotheses guarantee that if 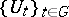 is an isometric representation of
is an isometric representation of 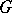 that is continuous in the weak topology, then for each finite regular Borel measure
that is continuous in the weak topology, then for each finite regular Borel measure 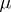 on
on 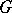 there is an operator
there is an operator 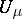 on
on 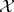 such that
such that 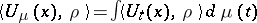 ,
, 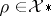 .
.
Arveson also considers pairs of such pairs, 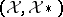 and
and  , and places additional hypotheses on each to ensure that the space of weakly continuous mappings from
, and places additional hypotheses on each to ensure that the space of weakly continuous mappings from 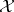 to
to 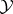 ,
, 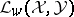 , with the operator norm, is in the same kind of duality with the closed linear span of the functionals of the form
, with the operator norm, is in the same kind of duality with the closed linear span of the functionals of the form 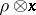 , where
, where 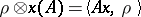 ,
,  ,
, 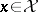 ,
, 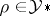 . (This space of the functionals will be denoted
. (This space of the functionals will be denoted  .) The reason for this is that he wants to study representations of
.) The reason for this is that he wants to study representations of 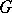 ,
, 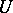 and
and 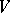 on
on 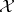 and
and 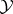 , respectively, and wants to focus on the representation
, respectively, and wants to focus on the representation 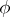 of
of  on
on 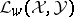 that they induce via the formula
that they induce via the formula 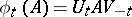 ,
, 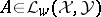 . The additional hypotheses that he assumes, then, are:
. The additional hypotheses that he assumes, then, are:
i) 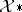 is a norm-closed subspace of the Banach space dual of
is a norm-closed subspace of the Banach space dual of 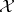 , and similarly for
, and similarly for 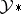 and
and 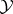 ; and
; and
ii) relative to the 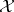 -topology on
-topology on 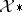 , the closed convex hull of every compact set in
, the closed convex hull of every compact set in 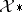 is compact. He then restricts his attention to representations
is compact. He then restricts his attention to representations 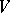 of
of 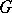 on
on 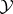 such that for each
such that for each 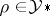 ,
,  is continuous with respect to the norm on
is continuous with respect to the norm on 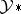 . Under these assumptions,
. Under these assumptions, 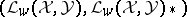 satisfy the hypotheses of the previous paragraph and
satisfy the hypotheses of the previous paragraph and 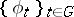 is weakly continuous.
is weakly continuous.
Returning to the case of the pair 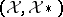 and
and 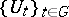 satisfying the hypotheses above, let
satisfying the hypotheses above, let 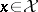 and consider the space
and consider the space 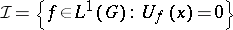 , where
, where 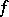 is identified with the measure that is
is identified with the measure that is 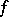 times Haar measure. Then
times Haar measure. Then 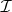 is a closed ideal in
is a closed ideal in 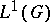 that is proper, if
that is proper, if 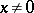 , by an approximate identity argument. The hull of
, by an approximate identity argument. The hull of 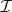 , which, by definition, is the intersection of the zero sets of the Fourier transforms of the functions in
, which, by definition, is the intersection of the zero sets of the Fourier transforms of the functions in 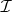 , is a closed subset of the dual group
, is a closed subset of the dual group 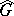 that is non-empty if
that is non-empty if 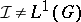 , i.e., if
, i.e., if 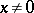 , by the Tauberian theorem (cf. also Tauberian theorems). This hull is called the (Arveson) spectrum of
, by the Tauberian theorem (cf. also Tauberian theorems). This hull is called the (Arveson) spectrum of  and is denoted by
and is denoted by 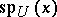 . A moment's reflection reveals that
. A moment's reflection reveals that  coincides with the set discussed at the outset when
coincides with the set discussed at the outset when 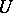 is a representation of
is a representation of 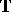 .
.
For each closed subset  , let
, let
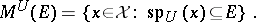 |
Then 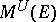 is a closed subspace of
is a closed subspace of 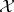 that is invariant under
that is invariant under 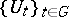 and is called the spectral subspace determined by
and is called the spectral subspace determined by 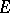 . It can be shown that if
. It can be shown that if 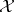 is a Hilbert space, so that
is a Hilbert space, so that 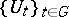 is a unitary representation of
is a unitary representation of 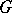 with spectral measure
with spectral measure 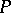 on
on 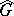 , then
, then 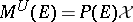 . Thus, the spectral subspaces
. Thus, the spectral subspaces  generalize to arbitrary Banach spaces and isometry groups, satisfying the basic assumptions above, giving the familiar spectral subspaces of unitary representations. They are defined, however, only for closed subsets of
generalize to arbitrary Banach spaces and isometry groups, satisfying the basic assumptions above, giving the familiar spectral subspaces of unitary representations. They are defined, however, only for closed subsets of 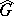 and do not, in general, have the nice lattice-theoretic properties of the spectral subspaces for unitary representations. Nevertheless, they have proved to be immensely useful in analyzing group representations of Abelian groups.
and do not, in general, have the nice lattice-theoretic properties of the spectral subspaces for unitary representations. Nevertheless, they have proved to be immensely useful in analyzing group representations of Abelian groups.
The principal contribution of Arveson in this connection is a result that generalizes a theorem of F. Forelli [a5] that relates the spectral subspaces of  ,
, 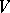 , and
, and 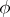 , in the setting described above. To state it, suppose
, in the setting described above. To state it, suppose  is a closed subset of
is a closed subset of  that contains
that contains  and let
and let 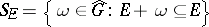 . Then
. Then 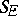 is an additive semi-group, containing
is an additive semi-group, containing  and contained in
and contained in 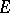 , that coincides with
, that coincides with 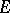 if
if 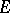 is a sub-semi-group of
is a sub-semi-group of 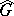 . Now assume the hypotheses i)–ii). Arveson proves [a1], Thm. 2.3, that if a closed subset
. Now assume the hypotheses i)–ii). Arveson proves [a1], Thm. 2.3, that if a closed subset 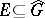 and an operator
and an operator 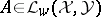 are given, then
are given, then 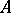 lies in
lies in 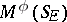 if and only if
if and only if 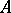 maps
maps 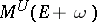 into
into  for every
for every 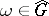 .
.
The principal application of Arveson's theorem is to this very general set up: Suppose  is a
is a 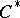 -algebra (respectively, a von Neumann algebra) and that
-algebra (respectively, a von Neumann algebra) and that 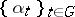 is an action of
is an action of 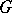 by automorphisms that is strongly continuous (respectively, ultraweakly continuous). Let
by automorphisms that is strongly continuous (respectively, ultraweakly continuous). Let 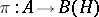 be a
be a 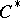 -representation (that is ultraweakly continuous when
-representation (that is ultraweakly continuous when 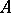 is a von Neumann algebra) and let
is a von Neumann algebra) and let 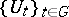 be a strongly continuous unitary representation of
be a strongly continuous unitary representation of 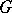 on
on 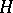 . The problem is to determine when the pair
. The problem is to determine when the pair 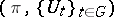 is a covariant representation in the sense that
is a covariant representation in the sense that 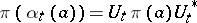 for all
for all 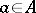 and
and 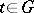 . Covariant representations play an important role throughout operator algebra and in particular in its applications to physics. In the particular case when
. Covariant representations play an important role throughout operator algebra and in particular in its applications to physics. In the particular case when  , one finds on the basis of Arveson's theorem that
, one finds on the basis of Arveson's theorem that 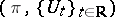 is a covariant representation if and only if
is a covariant representation if and only if 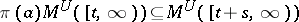 for all
for all 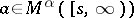 .
.
Arveson applied this theorem to re-prove and improve a number of theorems in the literature. It has come to be a standard tool and nowadays (1998) spectral subspaces are ubiquitous in operator algebra. (See [a2] for an expanded survey.) Of particular note is the notion of the Connes spectrum of an automorphism group [a4], which is based on the Arveson spectrum. The Connes spectrum is a very powerful conjugacy invariant of the group that has played a fundamental role in the classification of von Neumann algebras.
References
| [a1] | W. Arveson, "On groups of automorphisms of operator algebras" J. Funct. Anal. , 13 (1974) pp. 217–243 |
| [a2] | W. Arveson, "The harmonic analysis of automorphism groups" , Operator Algebras and Automorphisms , Proc. Symp. Pure Math. , 38: 1 , Amer. Math. Soc. (1982) pp. 199–269 |
| [a3] | A. Beurling, "On the spectral synthesis of bounded functions" Acta Math. , 81 (1949) pp. 225–238 |
| [a4] | A. Connes, "Une classification des facteurs de type III" Ann. Sci. Ecole Norm. Sup. 4 , 6 (1973) pp. 133–252 |
| [a5] | F. Forelli, "Analytic and quasi-invariant measures" Acta Math. , 118 (1967) pp. 33–59 |
| [a6] | R. Godement, "Théorèmes taubériens et théorie spectrale" Ann. Sci. Ecole Norm. Sup. 3 , 63 (1947) pp. 119–138 |
| [a7] | Y. Katznelson, "An introduction to harmonic analysis" , Wiley (1968) |
Arveson spectrum. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Arveson_spectrum&oldid=13072